题目内容
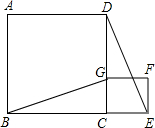 如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
(1)①求证:BG=DE;②图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
(2)若正方形ABCD的边长是1,延长BG恰好交于DE的中点M,求DC+CE的值.
 解:(1)①∵BC=DC,
解:(1)①∵BC=DC,∠BCG=∠DCE=90°,
CG=CE,
∴△BCG≌△DCE(SAS),(3分)
∴BG=DE;
②存在,△BCG≌△DCE,①中已证明,且△BCG和△DCE有共同顶点C,则△DCE沿C点旋转向左90°与△BCG重合;
(2)连接BD.
BD=
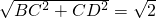 ;
;∵△BCG≌△DCE,
∴∠CBG=∠CDE;
又∵∠CDE+∠MEC=90°,
∴∠CBG+∠MEC=90°,
∴BM⊥DE,
又∵M是DE的中点,
∴BE=BD=
 ,
,∴DC+CE=BC+CE=
 .
.分析:(1)①根据已知,利用SAS判定△BCG≌△DCE,全等三角形的对应边相等,所以BG=DE;②存在,△BCG和△DCE可以通过旋转重合.求证△BCG≌△DCE即可;
(2)因为CD=BC,所以可以将问题求DC+CE的值转化为求BC+CE的值.连接BD.利用勾股定理求正方形ABCD的对角线BD=
 ,利用①中的全等三角形△BCG≌△DCE的对应角相等∠CBG=∠CDE;又有直角三角形的两个锐角互余知∠CDE+∠MEC=90°,利用等量代换求得∠CBG+∠MEC=90°,即BM⊥DE;然后由等腰三角形的性质解答即可.
,利用①中的全等三角形△BCG≌△DCE的对应角相等∠CBG=∠CDE;又有直角三角形的两个锐角互余知∠CDE+∠MEC=90°,利用等量代换求得∠CBG+∠MEC=90°,即BM⊥DE;然后由等腰三角形的性质解答即可.点评:本题考查了全等三角形判定与性质、正方形的性质(各边相等且各内角为90°)、旋转的性质及勾股定理的应用.本题中求证△BCG≌△DCE是解题的关键,另外,作辅助线BD,将问题求DC+CE的值转化为求BC+CE的值,降低了题的难度与梯度.

练习册系列答案
相关题目
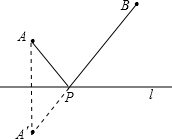 几何模型:条件:如图,A、B是直线l同旁的两个定点.
几何模型:条件:如图,A、B是直线l同旁的两个定点.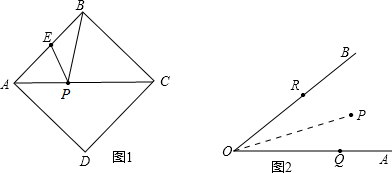
 8、如图所示,∠A与∠B是
8、如图所示,∠A与∠B是
 如图所示,∠1和∠3是直线
如图所示,∠1和∠3是直线
 (n表示的正整数)时,S△ABC=6n,S△DBC=n(n+5),求S△PBC
(n表示的正整数)时,S△ABC=6n,S△DBC=n(n+5),求S△PBC