题目内容
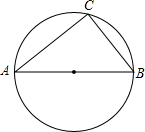 如图,AB是⊙O的直径,弦BC=4cm,∠ABC=60°.
如图,AB是⊙O的直径,弦BC=4cm,∠ABC=60°.
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连接CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E从A点出发沿着AB方向运动,同时动点F从B点出发沿BC方向运动,设AE=x、BF=y,连接EF,求当△BEF为直角三角形时,写出x、y的关系式,(不要求写出x的取值范围).
解:(1)∵AB是⊙O的直径,∴∠C=90°,
又弦BC=4cm,∠ABC=60°,∴∠A=30°,
则⊙O的直径AB=2BC=8cm;
(2)根据题意画出图形,如图所示:
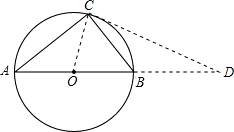 当BD=BC=4cm时,CD与圆O的相切,
当BD=BC=4cm时,CD与圆O的相切,
证明:∵∠ABC=60°,OC=OB,
∴△OCB为等边三角形,∴CB=OB=BD,
∴∠OCD=90°,
∴CD是圆O的切线;
(3)当∠EFB=90°时,画出图形得:
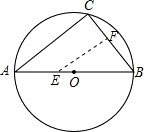 由AB为圆O的直径得到∠C=90°,又∠B=60°,
由AB为圆O的直径得到∠C=90°,又∠B=60°,
∴∠A=30°,则AB=2BC=8,
∵∠EFB=∠C=90°,∠B=∠B,
∴△EFB∽△ACB,
∴ =
= ,即
,即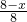 =
= ,
,
∴y=- x+4;
x+4;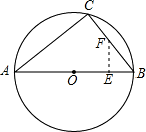
当∠FEB=90°时,画出图形得:
由∠B=∠B,∠FEB=∠C=90°,
∴△FEB∽△ACB,
∴ =
= ,即
,即 =
= ,
,
∴y=-2x+16.
分析:(1)由AB为圆O的直径,根据直径所对的圆周角为直角得到∠C=90°,又∠ABC=60°得到∠A=30°,根据30°角所对的直角边等于斜边的一半,由BC求出AB的长,即为圆O的直径;
(2)根据题意画出图形,当DB=OB时,CD与圆O相切,理由为:由OC=OB得到△OCB为等腰三角形,又∠ABC为60°,故△OCB为等边三角形,进而得到CB=OB=OC,而OB=BD,故CB=OB=BD,根据一边上的中线等于这边的一半,得到这边所对的角为直角,即∠OCD为直角,故DC与圆O相切;
(3)分∠EFB为直角和∠FEB为直角两种情况考虑,由AB和BC的长,以及设出的AE=x,BF=y,利用三角形的相似即可表示出各自的y与x的函数关系式.
点评:此题综合考查了切线的性质,圆周角定理及相似三角形的判断与性质.其中证明切线的方法有:1、有点连接此点与半径,证明夹角为直角;2、无点作垂线,证明垂线段等于半径.动点问题注意审清题意,利用分类讨论及数形结合的数学思想解决问题.
又弦BC=4cm,∠ABC=60°,∴∠A=30°,
则⊙O的直径AB=2BC=8cm;
(2)根据题意画出图形,如图所示:
 当BD=BC=4cm时,CD与圆O的相切,
当BD=BC=4cm时,CD与圆O的相切,证明:∵∠ABC=60°,OC=OB,
∴△OCB为等边三角形,∴CB=OB=BD,
∴∠OCD=90°,
∴CD是圆O的切线;
(3)当∠EFB=90°时,画出图形得:
 由AB为圆O的直径得到∠C=90°,又∠B=60°,
由AB为圆O的直径得到∠C=90°,又∠B=60°,∴∠A=30°,则AB=2BC=8,
∵∠EFB=∠C=90°,∠B=∠B,
∴△EFB∽△ACB,
∴
 =
= ,即
,即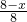 =
= ,
,∴y=-
 x+4;
x+4;
当∠FEB=90°时,画出图形得:
由∠B=∠B,∠FEB=∠C=90°,
∴△FEB∽△ACB,
∴
 =
= ,即
,即 =
= ,
,∴y=-2x+16.
分析:(1)由AB为圆O的直径,根据直径所对的圆周角为直角得到∠C=90°,又∠ABC=60°得到∠A=30°,根据30°角所对的直角边等于斜边的一半,由BC求出AB的长,即为圆O的直径;
(2)根据题意画出图形,当DB=OB时,CD与圆O相切,理由为:由OC=OB得到△OCB为等腰三角形,又∠ABC为60°,故△OCB为等边三角形,进而得到CB=OB=OC,而OB=BD,故CB=OB=BD,根据一边上的中线等于这边的一半,得到这边所对的角为直角,即∠OCD为直角,故DC与圆O相切;
(3)分∠EFB为直角和∠FEB为直角两种情况考虑,由AB和BC的长,以及设出的AE=x,BF=y,利用三角形的相似即可表示出各自的y与x的函数关系式.
点评:此题综合考查了切线的性质,圆周角定理及相似三角形的判断与性质.其中证明切线的方法有:1、有点连接此点与半径,证明夹角为直角;2、无点作垂线,证明垂线段等于半径.动点问题注意审清题意,利用分类讨论及数形结合的数学思想解决问题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为