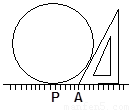题目内容
 为了测量一个圆形铁环的半径,小华采用了如下方法:将铁环平放在水平桌面上,用一个锐角为30°的直角三角板和一个刻度尺,按如图所示的方法得到有关数据,进而求得铁环的半径,若测得AB=10cm,则铁环的半径是
为了测量一个圆形铁环的半径,小华采用了如下方法:将铁环平放在水平桌面上,用一个锐角为30°的直角三角板和一个刻度尺,按如图所示的方法得到有关数据,进而求得铁环的半径,若测得AB=10cm,则铁环的半径是10
cm
| 3 |
10
cm
.| 3 |
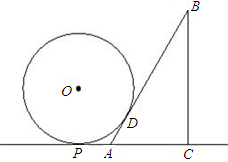
分析:由铁环与桌面及AE边相切,根据切线的性质得到OB与AB垂直,OC与AC垂直,再由AB与AC都为圆O的切线,根据切线长定理得到OA为角平分线,可得出∠AOB=∠AOC,再由一对直角相等,根据三角形的内角和定理得出∠OAB=∠OAC,由直角三角形AED中∠E=30°,根据直角三角形的两锐角互余得到求出∠EAD的度数,进而得出邻补角∠BAC的度数,确定出∠OAB的度数,在直角三角形OAB中,由AB的长及tan∠OAB的值,利用锐角三角函数定义求出OB的长,即为圆O的半径.
解答:解:如图所示:连接OB,OC,OA,

∵AB为圆O的切线,
∴OB⊥AB,即∠OBA=90°,
又AC为圆O的切线,
∴OC⊥AC,即∠OCA=90°,
在Rt△ADE中,∠E=30°,∠ADE=90°,
∴∠EAD=60°,∠BAC=120°,
∵AC及AB为圆O的切线,
∴OA为∠BOC的平分线,即∠BOA=∠COA,
又∠OBA=∠OCA=90°,
∴∠OAB=∠OAC=
∠BAC=60°,
在Rt△OBA中,∠OBA=90°,∠OAB=60°,AB=10cm,
∴tan60°=
,即
=
,
则圆的半径OB=10
cm.
故答案为:10
cm

∵AB为圆O的切线,
∴OB⊥AB,即∠OBA=90°,
又AC为圆O的切线,
∴OC⊥AC,即∠OCA=90°,
在Rt△ADE中,∠E=30°,∠ADE=90°,
∴∠EAD=60°,∠BAC=120°,
∵AC及AB为圆O的切线,
∴OA为∠BOC的平分线,即∠BOA=∠COA,
又∠OBA=∠OCA=90°,
∴∠OAB=∠OAC=
| 1 |
| 2 |
在Rt△OBA中,∠OBA=90°,∠OAB=60°,AB=10cm,
∴tan60°=
| OB |
| AB |
| 3 |
| OB |
| 10 |
则圆的半径OB=10
| 3 |
故答案为:10
| 3 |
点评:此题考查了切线的性质,切线长定理,锐角三角函数定义,以及三角形的内角和定理,是一道与实际生活密切相关的题型,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 为了测量一个圆形铁环的半径,某同学采用如下方法:将铁环平放在水平的桌面上,用一个锐角为30°的三角板和一个刻度尺,按照如图(1)的方法(其中铁环与三角板的斜边相切)得到相关数据,进而求得铁环的半径.
为了测量一个圆形铁环的半径,某同学采用如下方法:将铁环平放在水平的桌面上,用一个锐角为30°的三角板和一个刻度尺,按照如图(1)的方法(其中铁环与三角板的斜边相切)得到相关数据,进而求得铁环的半径.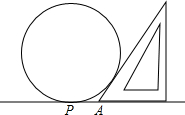 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径.
为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径. 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是( )cm.
为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是( )cm.