题目内容
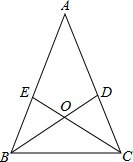 我们称顶角为36°的等腰三角形为“黄金三角形”.如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A,∠ABC、∠ACB的角平分线BD、CE交于点O,则图中的“黄金三角形”共有个.
我们称顶角为36°的等腰三角形为“黄金三角形”.如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A,∠ABC、∠ACB的角平分线BD、CE交于点O,则图中的“黄金三角形”共有个.
- A.3
- B.4
- C.5
- D.6
C
分析:由在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用“黄金三角形”的定义,即可判定△ABC,△BDC,△BCE,△OBE,△OCD都是“黄金三角形”.
解答: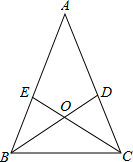 解:∵在△ABC中,AB=AC,∠A=36°,
解:∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°-∠A)÷2=72°,
∵△ABC的角平分线BD与CE相交于点O,
∴∠ABD=∠DBC= ∠ABC=36°,∠ACE=∠BCE=
∠ABC=36°,∠ACE=∠BCE= ∠ACB=36°,
∠ACB=36°,
∴∠BEC=∠BDC=180°-36°-72°=72°,
∴∠A=∠EBO=∠DBC=∠DCO=36°,∠ABC=∠ACB=∠BEC=∠BDC=72°,
∴∠EOB=∠DOC=180°-72°-36°=72°,
∴BE=OB=OC=CD,CE=BC=BD,
∴“黄金三角形”有:△ABC,△BDC,△BCE,△OBE,△OCD共5个.
故选C.
点评:此题考查了学生读题做题的能力以及等腰三角形的性质与判定.此题难度适中,正确理解“黄金三角形”的定义是解题的关键.
分析:由在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用“黄金三角形”的定义,即可判定△ABC,△BDC,△BCE,△OBE,△OCD都是“黄金三角形”.
解答:
 解:∵在△ABC中,AB=AC,∠A=36°,
解:∵在△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=(180°-∠A)÷2=72°,
∵△ABC的角平分线BD与CE相交于点O,
∴∠ABD=∠DBC=
 ∠ABC=36°,∠ACE=∠BCE=
∠ABC=36°,∠ACE=∠BCE= ∠ACB=36°,
∠ACB=36°,∴∠BEC=∠BDC=180°-36°-72°=72°,
∴∠A=∠EBO=∠DBC=∠DCO=36°,∠ABC=∠ACB=∠BEC=∠BDC=72°,
∴∠EOB=∠DOC=180°-72°-36°=72°,
∴BE=OB=OC=CD,CE=BC=BD,
∴“黄金三角形”有:△ABC,△BDC,△BCE,△OBE,△OCD共5个.
故选C.
点评:此题考查了学生读题做题的能力以及等腰三角形的性质与判定.此题难度适中,正确理解“黄金三角形”的定义是解题的关键.

练习册系列答案
相关题目
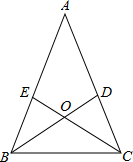 我们称顶角为36°的等腰三角形为“黄金三角形”.如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A,∠ABC、∠ACB的角平分线BD、CE交于点O,则图中的“黄金三角形”共有( )个.
我们称顶角为36°的等腰三角形为“黄金三角形”.如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A,∠ABC、∠ACB的角平分线BD、CE交于点O,则图中的“黄金三角形”共有( )个.