题目内容
 如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.证明:DE是圆O的切线.
分析:连结OD,易得OD为△ABC的中位线,根据中位线性质得OD∥BC,而DE⊥BC,根据平行线性质得DE⊥OD,于是可根据切线的判定定理得到DE是圆O的切线.
解答:证明: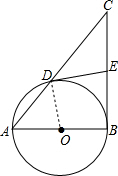 连结OD,如图,
连结OD,如图,
∵AB是圆O的直径,
∴O点为AB的中点,
∵点D为AC的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∴DE是圆O的切线.
 连结OD,如图,
连结OD,如图,∵AB是圆O的直径,
∴O点为AB的中点,
∵点D为AC的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∴DE是圆O的切线.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了三角形中位线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 四边形是平行四边形.
四边形是平行四边形. x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).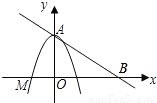
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).