题目内容
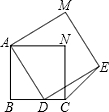
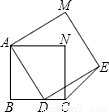
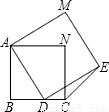
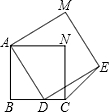 如图是分别由两个具有公共顶点A的正方形组成的图形,且其中一个正方形的顶点在另一个正方形的边BC上(点D不与点B、C重合).则∠DCE=________.
如图是分别由两个具有公共顶点A的正方形组成的图形,且其中一个正方形的顶点在另一个正方形的边BC上(点D不与点B、C重合).则∠DCE=________.
135°
分析:首先作辅助线EH⊥BC于H,通过求证△DEH≌△ABD,推出EH=BD,DH=AB=BC,即得,CH=BD=EH,由EH⊥BC,推出△ECH为等腰直角三角形,即得,∠ECH=45°,即可推出结论.
解答: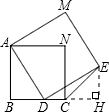 解:作EH⊥BC于H,
解:作EH⊥BC于H,
∵正方形ABCN,正方形ADEM,
∴∠ADE=∠ABD=90°,
∴∠BAD+∠ADB=90°,∠EDH+∠ADB=90°,
∴∠EDH=∠BAD,
又∵AD=DE,∠DHE=∠DBA=90°,
∴△DEH≌△ABD,
∴EH=BD,DH=AB=BC,
∴CH=BD=EH,
∵∠DHE=90°,
∴∠ECH=45°,
∴∠DCE=135°.
故答案为135°.
点评:本题主要考查全等三角形的判定与性质、邻补角的性质、正方形的性质,关键在于根据已知推出△DEH≌△ABD,根据三角形全等推出△ECH为等腰直角三角形.
分析:首先作辅助线EH⊥BC于H,通过求证△DEH≌△ABD,推出EH=BD,DH=AB=BC,即得,CH=BD=EH,由EH⊥BC,推出△ECH为等腰直角三角形,即得,∠ECH=45°,即可推出结论.
解答:
 解:作EH⊥BC于H,
解:作EH⊥BC于H,∵正方形ABCN,正方形ADEM,
∴∠ADE=∠ABD=90°,
∴∠BAD+∠ADB=90°,∠EDH+∠ADB=90°,
∴∠EDH=∠BAD,
又∵AD=DE,∠DHE=∠DBA=90°,
∴△DEH≌△ABD,
∴EH=BD,DH=AB=BC,
∴CH=BD=EH,
∵∠DHE=90°,
∴∠ECH=45°,
∴∠DCE=135°.
故答案为135°.
点评:本题主要考查全等三角形的判定与性质、邻补角的性质、正方形的性质,关键在于根据已知推出△DEH≌△ABD,根据三角形全等推出△ECH为等腰直角三角形.

练习册系列答案
相关题目
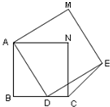 13、如图是分别由两个具有公共顶点A的正方形组成的图形,且其中一个正方形的顶点在另一个正方形的边BC上(点D不与点B、C重合).则∠DCE=
13、如图是分别由两个具有公共顶点A的正方形组成的图形,且其中一个正方形的顶点在另一个正方形的边BC上(点D不与点B、C重合).则∠DCE=