题目内容
(2002•山西)已知:抛物线y=ax2+bx与x铀的一个交点为B,顶点A在直线y=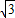 x上,O为坐标原点.
x上,O为坐标原点.(1)证明:△OAB为等边三角形;
(2)若△OAB的内切圆半径为1,求出抛物线的解析式;
(3)在抛物线上是否存在点P,使△POB是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
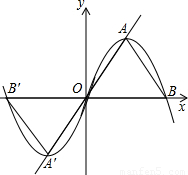
【答案】分析:(1)根据直线OA的斜率不难得到∠AOB=60°,根据抛物线的对称性可知AB=OA,由此得证.
(2)由于抛物线的开口方向不确定,因此分a>0和a<0两种情况求解.以a<0为例说明:
可设三角形AOB的内心为I,过A作AC⊥OB,则I必在AC上,连接IO,在构建的直角三角形IOC中,∠IOC=30°,已知了IC=1,即可求出OC和IO的长,也就能求出B点和A点的坐标,然后将这两点坐标代入抛物线中即可求出二次函数的解析式.(a>0时,解法完全相同).
(3)如果△POB是直角三角形,那么如果过P作x轴的垂线,根据射影定理即可得出P点纵坐标绝对值的平方等于P点横坐标绝对值和P、B两点横坐标差的绝对值的乘积.然后联立抛物线的解析式即可求出P点坐标.
解答: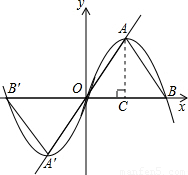 (1)证明:作AC⊥OB于点C;
(1)证明:作AC⊥OB于点C;
∵点A在直线y=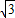 x上,设A(x,
x上,设A(x, x).
x).
在直角三角形OAC中,tan∠AOC=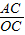 =
=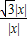 =
=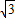 ,
,
∴∠AOC=60°
由抛物线的对称性可知:OA=AB,
∴△AOB为等边三角形.
(2)解:当a<0时,设△AOB的内心为I,则∠IOC=30°,在直角三角形IOC中,
∵IC=1,OC=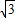 .
.
∴抛物线的对称轴x=-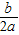 =
=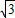 ,
,
∴a=-1,b=2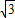 .
.
∴抛物线的解析式为y=-x2+2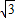 x.
x.
当a>0时,同法可求,另一条抛物线的解析式为y=x2+2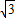 x.
x.
(3)解:易知:抛物线与x轴的两交点为O(0,0),B(-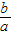 ,0).
,0).
且顶点A(-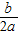 ,-
,-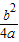 )在直线y=
)在直线y=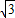 x上,
x上,
∴-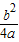 =
=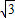 (-
(-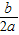 ),
),
解得b=2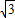 ,b=0(舍去).
,b=0(舍去).
∴B(-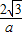 ,0)
,0)
抛物线的解析式为y=ax2+2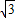 x.
x.
假设存在符合条件的点P(m,n).
过点P做PD⊥OB于D,则根据射影定理有: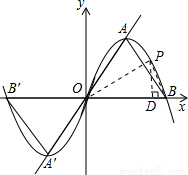
PD2=OD•BD;
由题意知:y=ax2+2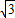 x,
x,
∴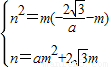 ,
,
解得: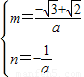 ,
,
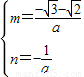 ,
,
∴存在符合条件的P点,且坐标为:P(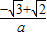 ,-
,-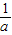 )或(
)或(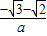 ,-
,-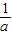 ).
).
点评:本题是二次函数综合题,考查了等边三角形的判定、二次函数解析式的确定、三角形内心等知识点.综合性强,难度较大.
(2)由于抛物线的开口方向不确定,因此分a>0和a<0两种情况求解.以a<0为例说明:
可设三角形AOB的内心为I,过A作AC⊥OB,则I必在AC上,连接IO,在构建的直角三角形IOC中,∠IOC=30°,已知了IC=1,即可求出OC和IO的长,也就能求出B点和A点的坐标,然后将这两点坐标代入抛物线中即可求出二次函数的解析式.(a>0时,解法完全相同).
(3)如果△POB是直角三角形,那么如果过P作x轴的垂线,根据射影定理即可得出P点纵坐标绝对值的平方等于P点横坐标绝对值和P、B两点横坐标差的绝对值的乘积.然后联立抛物线的解析式即可求出P点坐标.
解答:
 (1)证明:作AC⊥OB于点C;
(1)证明:作AC⊥OB于点C;∵点A在直线y=
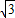 x上,设A(x,
x上,设A(x, x).
x).在直角三角形OAC中,tan∠AOC=
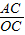 =
=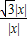 =
=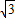 ,
,∴∠AOC=60°
由抛物线的对称性可知:OA=AB,
∴△AOB为等边三角形.
(2)解:当a<0时,设△AOB的内心为I,则∠IOC=30°,在直角三角形IOC中,
∵IC=1,OC=
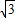 .
.∴抛物线的对称轴x=-
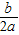 =
=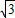 ,
,∴a=-1,b=2
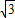 .
.∴抛物线的解析式为y=-x2+2
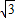 x.
x.当a>0时,同法可求,另一条抛物线的解析式为y=x2+2
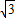 x.
x.(3)解:易知:抛物线与x轴的两交点为O(0,0),B(-
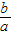 ,0).
,0).且顶点A(-
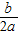 ,-
,-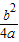 )在直线y=
)在直线y=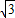 x上,
x上,∴-
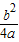 =
=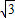 (-
(-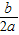 ),
),解得b=2
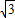 ,b=0(舍去).
,b=0(舍去).∴B(-
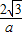 ,0)
,0)抛物线的解析式为y=ax2+2
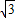 x.
x.假设存在符合条件的点P(m,n).
过点P做PD⊥OB于D,则根据射影定理有:

PD2=OD•BD;
由题意知:y=ax2+2
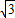 x,
x,∴
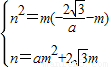 ,
,解得:
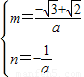 ,
,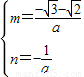 ,
,∴存在符合条件的P点,且坐标为:P(
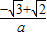 ,-
,-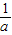 )或(
)或(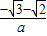 ,-
,-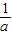 ).
).点评:本题是二次函数综合题,考查了等边三角形的判定、二次函数解析式的确定、三角形内心等知识点.综合性强,难度较大.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 x上,O为坐标原点.
x上,O为坐标原点.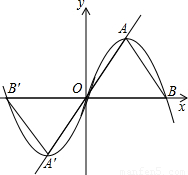
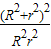 .
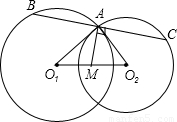
.
 .
.
 .
.