题目内容
 坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
- A.(0,0)
- B.(2,-1)
- C.(0,1)
- D.(2,1)
B
分析:根据题意找出圆心M的位置,得出M在AB和BC的垂直平分线的交点上,求出A的坐标,求出M的横坐标,根据AM=BM,根据勾股定理求出AM和BM,即可得出方程,求出方程的解即可.
解答: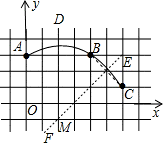
连接AB、BC,分别作AB和BC的垂直平分线DM、EF,两线交于M,则M为弧所在的圆的圆心,如图,
∵点B的坐标为(4,3),点C坐标为(6,1),
∴A的坐标是(0,3,),
∴M点的横坐标是2,设M的坐标为a,
∵M在AB的垂直平分线上,
∴MA=MB,
根据勾股定理得:22+(3-a)2=(4-2)2+(3-a)2
解得:a=-1,
即M的坐标是(2,-1),
故选B.
点评:本题考查了线段垂直平分线,垂径定理,勾股定理,坐标与图形性质等知识点,关键是找出M的位置,题目比较典型,是一道比较好的题目.
分析:根据题意找出圆心M的位置,得出M在AB和BC的垂直平分线的交点上,求出A的坐标,求出M的横坐标,根据AM=BM,根据勾股定理求出AM和BM,即可得出方程,求出方程的解即可.
解答:

连接AB、BC,分别作AB和BC的垂直平分线DM、EF,两线交于M,则M为弧所在的圆的圆心,如图,
∵点B的坐标为(4,3),点C坐标为(6,1),
∴A的坐标是(0,3,),
∴M点的横坐标是2,设M的坐标为a,
∵M在AB的垂直平分线上,
∴MA=MB,
根据勾股定理得:22+(3-a)2=(4-2)2+(3-a)2
解得:a=-1,
即M的坐标是(2,-1),
故选B.
点评:本题考查了线段垂直平分线,垂径定理,勾股定理,坐标与图形性质等知识点,关键是找出M的位置,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
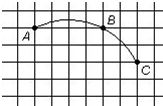 14、坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
14、坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
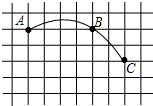 (2012•路北区一模)坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为( )
(2012•路北区一模)坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为( )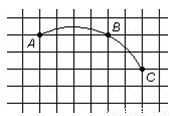
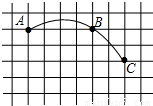 坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为( )
坐标网格中一段圆弧经过点A、B、C,其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为( )