Question

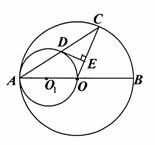
如图：AB是⊙O的直径，以OA为直径的⊙O₁与⊙O的弦AC相交于D，DE⊥OC，垂足为E。

（1）求证：AD＝DC

（2）求证：DE是的切线

（3）如果OE＝EC，请判断四边形O₁OED是什么四边形，并证明你的结论。

 

Answer 1

证明：（1）连结OD，则∠ADO＝90°

∵AC为⊙O的弦，OD为弦心距， ∴ AD＝DC         ……………………3分

（2）∵D为AC的中点，O₁为AO的中点，∴O₁D∥OC

     又DE⊥OC，∴DE⊥O₁D    ∴  DE与⊙O₁相切  ……………………6分

（3）如果OE＝EC ，又D为AC的中点

     ∴ DE∥O₁O   又O₁D∥OE  四边形为平行四边形

     又∠DEO＝90°，O₁O＝O₁D  ∴四边形O₁OED为正方形………………10分