题目内容
有以下四个说法:①两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;②两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;③两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等;④刘徽计算过π的值,认为其为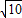 .其中正确的有( )
.其中正确的有( )A.1个
B.2个
C.3个
D.4个
【答案】分析:根据三角形全等的判定,利用排除法求解.
解答:解:①第三边上的中线对应相等时,可利用“SSS”证明全等,故本选项正确;
②没两角和其中一角的角平分线(或第三角的角平分线)对应相等,可利用“AAS”或“ASA”证明全等,故本选项正确;
③两边和其中一边上的高(或第三边上的高)对应相等,不能运用“SSA”证明两个三角形全等,故本选项错误;
④刘徽计算过π的值,认为其为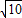 ,错误.
,错误.
所以有①②两项正确.
故选B.
点评:本题主要考查三角形全等的判定,根据三角形全等判定的方法找寻条件,如果符合就全等,否则就不全等.
解答:解:①第三边上的中线对应相等时,可利用“SSS”证明全等,故本选项正确;
②没两角和其中一角的角平分线(或第三角的角平分线)对应相等,可利用“AAS”或“ASA”证明全等,故本选项正确;
③两边和其中一边上的高(或第三边上的高)对应相等,不能运用“SSA”证明两个三角形全等,故本选项错误;
④刘徽计算过π的值,认为其为
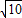 ,错误.
,错误.所以有①②两项正确.
故选B.
点评:本题主要考查三角形全等的判定,根据三角形全等判定的方法找寻条件,如果符合就全等,否则就不全等.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
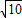 .其中正确的有( )
.其中正确的有( )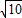 .其中正确的有( )
.其中正确的有( )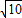 .其中正确的有( )
.其中正确的有( )