题目内容
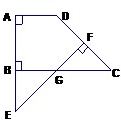19、已知：如图，在直角梯形ABCD中，AD∥BC，∠A=90°，∠C=45°，上底AD=8，AB=12，CD边的垂直平分线交BC边于点G，且交AB的延长线于点E，求AE的长．分析：由EF是CD的垂直平分线，∠C=45°，得到△DGC和BGE为等腰直角三角形，由此得到四边形ABGD是矩形，得到BG=AD=8，则BE=8，所以AE=AB+BE=12+8=20．
解答：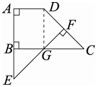
解：连接DG，如图，
∵EF是CD的垂直平分线，
∴DG=CG，
∴∠GDC=∠C，且∠C=45°，
∴∠DGC=90°，
∵AD∥BC，∠A=90°，
∴∠ABC=90°，
∴四边形ABGD是矩形，
∴BG=AD=8，
∴∠FGC=∠BGE=∠E=45°，
∴BE=BG=8，
∴AE=AB+BE=12+8=20．
解：连接DG，如图，∵EF是CD的垂直平分线，
∴DG=CG，
∴∠GDC=∠C，且∠C=45°，
∴∠DGC=90°，
∵AD∥BC，∠A=90°，
∴∠ABC=90°，
∴四边形ABGD是矩形，
∴BG=AD=8，
∴∠FGC=∠BGE=∠E=45°，
∴BE=BG=8，
∴AE=AB+BE=12+8=20．
点评：本题考查了直角梯形的性质；也考查了线段的垂直平分线的性质和等腰直角三角形的性质．
练习册系列答案
相关题目
