题目内容
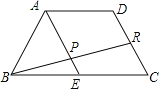
【题目】如图，AD∥BC，BC=2AD，E为BC的中点，R为DC的中点，BR交AE于点P，则EP：AP= ．
【答案】
．
【解析】
试题分析：先由BC=2AD，BE=EC=
BC，得出BE=EC=AD，根据AD∥BC，由一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形，那么EA=CD，EA∥CD．得出△BEP∽△BCR，于是EP=CR，而CR=CD，那么EP=
CD=EA，然后根据比例的性质即可求出答案即可．
解：∵BC=2AD，BE=EC=BC，
∴BE=EC=AD，
∵在等腰梯形ABCD中，AD∥BC，
∴四边形ADCE是平行四边形，
∴EA=CD，EA∥CD，
∴△BEP∽△BCR，
∵BE=EC=BC，
∴EP=
CR，
∵CR=CD，
∴EP=
CD=EA，
∴
=，
∴EP：AP=．
故答案为：．
练习册系列答案
相关题目
