题目内容
||x||表示非负数x四舍五入到个位数字的结果,如||14.54||=15,则下列判断正确的是 (填正确判断的序号):①||3.48||=4;
②对于任何非负实数x,y,都有||x+y||=||x||+||y||;
③n为非负整数,如果n-0.5≤x<n+0.5,那么||x||=n;
④||2x+1||=4,则x的取值范围是1.25≤x<1.75.
【答案】分析:根据||x||表示非负数x四舍五入到个位数字的结果,如||14.54||=15,分别进行分析即可.
解答:解:∵||x||表示非负数x四舍五入到个位数字的结果,||14.54||=15,
∴①||3.48||=3;故此选项错误;
②对于任何非负实数x,y,都有||x+y||=||x||+||y||;当x=1.2,y=1.4时此等式不成立,故此选项错误;
③n为非负整数,如果n-0.5≤x<n+0.5,那么||x||=n;根据加减0.5后,不用进位,故此选项正确;
④||2x+1||=4,
∴3.5≤2x+1<4.5,
∴x的取值范围是1.25≤x<1.75.故此选项正确,
故答案为:③④.
点评:此题主要考查了一元一次不等式组的应用,根据不等式性质得出3.5≤2x+1<4.5,再求出是解题关键.
解答:解:∵||x||表示非负数x四舍五入到个位数字的结果,||14.54||=15,
∴①||3.48||=3;故此选项错误;
②对于任何非负实数x,y,都有||x+y||=||x||+||y||;当x=1.2,y=1.4时此等式不成立,故此选项错误;
③n为非负整数,如果n-0.5≤x<n+0.5,那么||x||=n;根据加减0.5后,不用进位,故此选项正确;
④||2x+1||=4,
∴3.5≤2x+1<4.5,
∴x的取值范围是1.25≤x<1.75.故此选项正确,
故答案为:③④.
点评:此题主要考查了一元一次不等式组的应用,根据不等式性质得出3.5≤2x+1<4.5,再求出是解题关键.

练习册系列答案
相关题目
我校“心动数学”社团活动小组,在网格纸上为学校的一块空地设计植树方案如下:
第k棵树种植在点第xk行yk列处,其中x1=1,y1=1,当k≥2时,
,
[a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点所在的行数是4,则所在的列数是( )
第k棵树种植在点第xk行yk列处,其中x1=1,y1=1,当k≥2时,
|
[a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点所在的行数是4,则所在的列数是( )
| A、401 | B、402 |
| C、2009 | D、2010 |
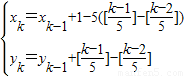 ,
,