题目内容
如图，反比例函数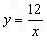
的图像与一次函数y＝kx＋4的图像相交于P、Q两点，并且P点的纵坐标是6．
（1 ）求这个一次函数的解析式
（2 ）求△POQ 的面积．
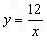的图像与一次函数y＝kx＋4的图像相交于P、Q两点，并且P点的纵坐标是6．（1 ）求这个一次函数的解析式
（2 ）求△POQ 的面积．
解:(1) 因点P 在反比例函数y=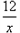
的图象上,且其纵坐标为6,于是,得
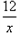=6,解得x=2,
∴P(2,6).
又∵点P 在函数y=kx+4 的图象上,
∴6=2k+4, 解得k=1.
∴所求一次函数解析式为y=x+4.
(2) 解方程组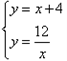
得
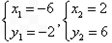
∴Q(-6,-2)令y=0, 代入y=x+4, 解得x=-4,
∴函数y=x+4 的图象与x 轴的交点是A(-4,0).
∴△AOP 和△AOQ 的公共边OA=4,OA 边上的高分别为PM=6,QN=2.
∴S△POQ=S△AOP+S△AOQ=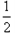
×4×6+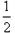
×4×2=16.
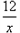的图象上,且其纵坐标为6,于是,得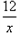=6,解得x=2,∴P(2,6).
又∵点P 在函数y=kx+4 的图象上,
∴6=2k+4, 解得k=1.
∴所求一次函数解析式为y=x+4.
(2) 解方程组
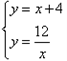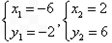
得 ∴Q(-6,-2)令y=0, 代入y=x+4, 解得x=-4,
∴函数y=x+4 的图象与x 轴的交点是A(-4,0).
∴△AOP 和△AOQ 的公共边OA=4,OA 边上的高分别为PM=6,QN=2.
∴S△POQ=S△AOP+S△AOQ=
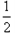×4×6+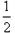×4×2=16. 
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
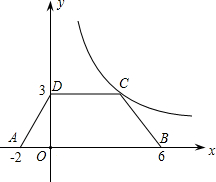（2012•南昌）如图，等腰梯形ABCD放置在平面坐标系中，已知A（-2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
（2013•和平区一模）如图，反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）．
（2012•湖里区一模）如图，反比例函数y=
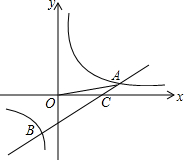已知：如图，反比例函数的图象和一次函数的图象交于A和B两点，且点A的坐标为（3，1），点B的坐标为（-1，-3），一次函数图象与X轴交于点C．连接OA．
的图象与直线
在第一象限交于点
，
为直线上的两点，点
的横坐标为2，点
的横坐标为3．
为反比例函数图象上的两点，且
平行于
轴．
的值；
的面积．