题目内容
猜想、探索规律(1)某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒…即每组所取种子数目比该组前一组增加2粒,按此规律,那么请你推测第100组应该有种子数.
(2)已知a1=
| 1 |
| 1×2×3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2×3×4 |
| 1 |
| 3 |
| 3 |
| 8 |
| 1 |
| 3×4×5 |
| 1 |
| 4 |
| 4 |
| 15 |
(3)下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,那么第101个图案中由

(4)观察下列各式:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2008×2009 |
分析:(1)第1组取3粒,第2组取5粒,第3组取7粒…第n组取(2n-1)粒解决问题;
(2)所有第一个加数分子是1,分母是三个连续自然数的乘积,第二个加数分子是1,分母是三个连续自然数中间的数,和的分母是三个连续自℃然数两端数的乘积,分子是三个连续自然数中间的数,因此可求得a99.
(3)第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,第3个图案由10个基础图形组成,…,第n个图案由(3n+1)个基础图形组成,由此解决问题;
(4)由
=1-
,
=
-
,
=
-
,…
=
-
,代入可解决问题.
(2)所有第一个加数分子是1,分母是三个连续自然数的乘积,第二个加数分子是1,分母是三个连续自然数中间的数,和的分母是三个连续自℃然数两端数的乘积,分子是三个连续自然数中间的数,因此可求得a99.
(3)第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,第3个图案由10个基础图形组成,…,第n个图案由(3n+1)个基础图形组成,由此解决问题;
(4)由
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:(1)第1组3=2×1+1,
第2组5=2×2+1,
第3组7=2×3+1,
…
第n组有2n+1粒,
所以第100组应该有种子2×100+1=201粒.
(2)由a1=
+
=
=
,
a2=
+
=
=
,
a3=
+
=
=
,
…
所以a99=
+
=
=
;
(3)第1个图案由4=4×1-(1-1)=3+1个基础图形组成,
第2个图案由7=4×2-(2-1)=3×2+1个基础图形组成,
第3个图案由10=4×3-(3-1)=3×3+1个基础图形组成,
…,
那么第101个图案中由3×101+1=304个基础图形组成;
(4)把
=1-
,
=
-
,
=
-
…代入得:
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
第2组5=2×2+1,
第3组7=2×3+1,
…
第n组有2n+1粒,
所以第100组应该有种子2×100+1=201粒.
(2)由a1=
| 1 |
| 1×2×3 |
| 1 |
| 2 |
| 2 |
| 1×3 |
| 2 |
| 3 |
a2=
| 1 |
| 2×3×4 |
| 1 |
| 3 |
| 3 |
| 2×4 |
| 3 |
| 8 |
a3=
| 1 |
| 3×4×5 |
| 1 |
| 4 |
| 4 |
| 3×5 |
| 4 |
| 15 |
…
所以a99=
| 1 |
| 99×100×101 |
| 1 |
| 100 |
| 100 |
| 99×101 |
| 100 |
| 9999 |
(3)第1个图案由4=4×1-(1-1)=3+1个基础图形组成,
第2个图案由7=4×2-(2-1)=3×2+1个基础图形组成,
第3个图案由10=4×3-(3-1)=3×3+1个基础图形组成,
…,
那么第101个图案中由3×101+1=304个基础图形组成;
(4)把
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2008×2009 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2008 |
| 1 |
| 2009 |
=1-
| 1 |
| 2009 |
=
| 2008 |
| 2009 |
点评:抓住式子的变化规律或数的变化规律,就可以解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
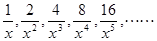 ,猜想并探索规律,那么第n个分式是
,猜想并探索规律,那么第n个分式是