题目内容
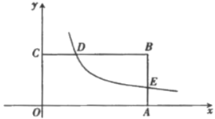
【题目】如图，在平面直角坐标系
中，矩形
的顶点
在
轴的正半轴上，顶点
在
轴的正半轴上，
是
边上的一点，
，
.反比例函数
在第一象限内的图像经过点，交
于点
，
.
(1)求这个反比例函数的表达式，
(2)动点
在矩形内，且满足
.
①若点在这个反比例函数的图像上，求点的坐标，
②若点
是平面内一点，使得以、
、、为顶点的四边形是菱形，求点的坐标.
【答案】（1）
；（2）① 
；②
【解析】
（1）设点B的坐标为（m，n），则点E的坐标为（m，
n），点D的坐标为（m6，n），利用反比例函数图象上点的坐标特征可求出m的值，结合OC：CD＝5：3可求出n值，再将m，n的值代入k＝mn中即可求出反比例函数的表达式；
（2）由三角形的面积公式、矩形的面积公式结合S△PAO＝
S四边形OABC可求出点P的纵坐标．
①若点P在这个反比例函数的图象上，利用反比例函数图象上点的坐标特征可求出点P的坐标；
②由点A，B的坐标及点P的纵坐标可得出AP≠BP，进而可得出AB不能为对角线，设点P的坐标为（t，4），分AP＝AB和BP＝AB两种情况考虑：（i）当AB＝AP时，利用勾股定理可求出t值，进而可得出点P1的坐标，结合P1Q1的长可求出点Q1的坐标；（ii）当BP＝AB时，利用勾股定理可求出t值，进而可得出点P2的坐标，结合P2Q2的长可求出点Q2的坐标．综上，此题得解．
解：（1）设点B的坐标为（m，n），则点E的坐标为（m，n），点D的坐标为（m6，n）．
∵点D，E在反比例函数
的图象上，
∴k＝mn＝（m6）n，
∴m＝9．
∵OC：CD＝5：3，
∴n：（m6）＝5：3，
∴n＝5，
∴k＝mn＝×9×5＝15，
∴反比例函数的表达式为y＝
；
（2）∵S△PAO＝S四边形OABC，
∴
OAyP＝OAOC，
∴yP＝
OC＝4．
①当y＝4时，＝4，
解得：x＝
，
∴若点P在这个反比例函数的图象上，点P的坐标为（，4）．
②由（1）可知：点A的坐标为（9，0），点B的坐标为（9，5），
∵yP＝4，yA＋yB＝5，
∴y P≠
，
∴AP≠BP，
∴AB不能为对角线．
设点P的坐标为（t，4）．
分AP＝AB和BP＝AB两种情况考虑（如图所示）：
（i）当AB＝AP时，（9t）2＋（40）2＝52，
解得：t1＝6，t2＝12（舍去），
∴点P1的坐标为（6，4），
又∵P1Q1＝AB＝5，
∴点Q1的坐标为（6，9）；
（ii）当BP＝AB时，（9t）2＋（51）2＝52，
解得：t3＝92
，t4＝9＋2（舍去），
∴点P2的坐标为（92，4）．
又∵P2Q2＝AB＝5，
∴点Q2的坐标为（92，1）．
综上所述：点Q的坐标为（6，9）或（92，1）．
