题目内容
【题目】如图1,已知正方形ABCD边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连结PQ、DQ、CQ、BQ.设AP﹦x.
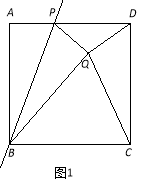

(1)BQ+DQ的最小值是 ,此时x的值是 ;
(2)如图2,若PQ的延长线交CD边于E,并且∠CQD=90°.
① 求证:QE﹦EC; ② 求x的值.
【答案】(1)![]() 或
或![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]()
【解析】
试题分析:(1)![]() 为点B到点D两段折线的和.由两点之间线段最短可知,连接DB,若点Q点落在BD上,此时和最短,且为
为点B到点D两段折线的和.由两点之间线段最短可知,连接DB,若点Q点落在BD上,此时和最短,且为![]() .考虑到动点运动,这种情形是存在的,由
.考虑到动点运动,这种情形是存在的,由![]() ,则
,则![]() ,
,![]() 所以
所以![]() ,即
,即![]() ,求解可得
,求解可得![]() ;
;
由已知条件对称分析,![]() ,则
,则![]() ,由
,由![]() ,可得
,可得![]() ,那么若有
,那么若有![]() ,则结论可证.再分析新条件
,则结论可证.再分析新条件![]() ,易得①结论.在
,易得①结论.在![]() 中,根据勾股定理列出方程,求出方程的解即可;
中,根据勾股定理列出方程,求出方程的解即可;
试题解析:(1)若点Q点落在BD上,此时和最短,且为![]() .
.![]() ,则
,则![]() ,
,![]()
![]() ,即
,即![]() ,解得
,解得![]() ;
;
①在正方形![]() 中,
中,![]() Q点为A点关于BP的对称点,
Q点为A点关于BP的对称点,![]()
![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 即
即![]() 为
为![]() 的中点;
的中点;
②![]()
![]() 在
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]()
![]()
![]() 解得
解得![]()

练习册系列答案
相关题目
【题目】近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
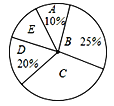
组别 | A | B | C | D | E |
时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
人数 | 12 | 30 | a | 24 | 12 |
(1)本次被调查的学生数是 人;
(2)统计表中a的值为 ;
(3)各组人数的众数是 ;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.