题目内容
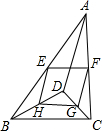 (2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是
(2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是11
11
.分析:利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=
AD,EF=GH=
BC,然后代入数据进行计算即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵BD⊥CD,BD=4,CD=3,
∴BC=
=
=5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=
AD,EF=GH=
BC,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=6,
∴四边形EFGH的周长=6+5=11.
故答案为:11.
∴BC=
| BD2+CD2 |
| 42+32 |
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=6,
∴四边形EFGH的周长=6+5=11.
故答案为:11.
点评:本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
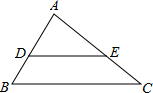 (2013•鞍山)如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
(2013•鞍山)如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )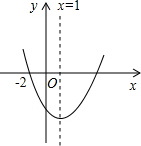 (2013•鞍山)如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:
(2013•鞍山)如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论: (2013•鞍山)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
(2013•鞍山)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的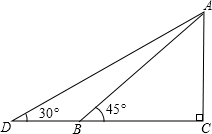 (2013•鞍山)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为
(2013•鞍山)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为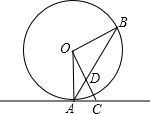 (2013•鞍山)如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
(2013•鞍山)如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.