题目内容
在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心、OB长为半径的圆交BC于D,DE⊥AC交AC于E.
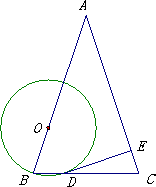
(1)求证:DE是⊙O的切线.
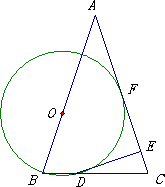
(2)若⊙O与AC相切于F,AB=AC=5 cm,![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
答案:
解析:
解析:
|
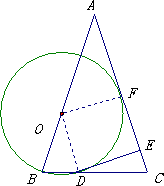
(1)证明:连接OD 1分 ∵OB=OD,∴∠B=∠ODB ∵AB=AC,∴∠B=∠C ∴∠ODB=∠C ∴OD∥AC 3分 又DE⊥AC ∴DE⊥OD ∴DE是⊙O的切线 4分 (2)解:如图,⊙O与AC相切于F点,连接OF,
|

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
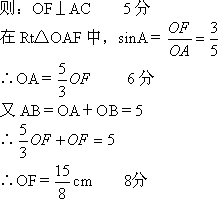
 如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=
如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=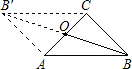 在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距
在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距 如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.
如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积. 如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是
如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是