题目内容
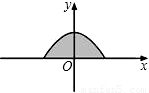
(附加题:如果你的全卷得分不足150分,则本题的得分记入总分,但记入总分后全卷得分不得超过150分,超过按150分算.)如图是二次函数y=-
 x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
【答案】分析:由于阴影部分为抛物线和坐标轴构成,初中阶段没有公式可利用,只能利用“(1)S在△ABC面积与过A、B、C三点的⊙O半圆面积之间,(2)这段图象在图示半径为 、2的两个半圆所夹的圆环内”的特点来进行估算其取值范围.
、2的两个半圆所夹的圆环内”的特点来进行估算其取值范围.
解答:解:
方法一:
由题意,可知这段图象与x轴的交点为A(-2,0)、B(2,0),与y轴的交点为C(0,2).(2分)
显然,S在△ABC面积与过A、B、C三点的⊙O半圆面积之间.(3分)
∵S△ABC=4,(4分)
 S⊙O=2π,(5分)
S⊙O=2π,(5分)
∴4<S<2π.(6分)
说明:关于半圆⊙O的面积大于图示阴影部分面积的证明,如下(对学生不要求):
设P(x,y)在图示抛物线上,则
OP2=x2+y2=(4-2y)+y2=(y-1)2+3.
∵0≤y≤2,
∴3≤OP2≤4.
∴点P在半圆x2+y2=3、x2+y2=4所夹的圆环内,以及点P为内圆周点( ,1)与外圆周点A、B、C.
,1)与外圆周点A、B、C.
∴半圆⊙O的面积大于图示阴影部分的面积.
由于内半圆的面积为 S⊙O-
S⊙O- ,
,
∴ <S<2π.
<S<2π.
如果学生能得出此结论,可在上面结论基础上,加(4分).
方法二:
由题意,可知这段图象与x轴的交点为A(-2,0)、B(2,0),与y轴的交点为C(0,2).(2分)
显然,这段图象在图示半径为 、2的两个半圆所夹的圆环内,以及过内半圆上点
、2的两个半圆所夹的圆环内,以及过内半圆上点
P( ,1)与半外圆上点A、B、C.(5分)
,1)与半外圆上点A、B、C.(5分)
∴S在图示两个半圆面积之间.(7分)
即 π•(
π•( )2<S<
)2<S< π•22.(9分)
π•22.(9分)
∴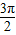 <S<2π.(10分)
<S<2π.(10分)
点评:此题考查了同学们的估算能力,用不同的图形为标准可得到不同的取值范围,有利于培养同学们的创新思维能力.当以后学习了积分,可直接求的阴影部分的准确值.
 、2的两个半圆所夹的圆环内”的特点来进行估算其取值范围.
、2的两个半圆所夹的圆环内”的特点来进行估算其取值范围.解答:解:
方法一:
由题意,可知这段图象与x轴的交点为A(-2,0)、B(2,0),与y轴的交点为C(0,2).(2分)
显然,S在△ABC面积与过A、B、C三点的⊙O半圆面积之间.(3分)
∵S△ABC=4,(4分)
 S⊙O=2π,(5分)
S⊙O=2π,(5分)∴4<S<2π.(6分)
说明:关于半圆⊙O的面积大于图示阴影部分面积的证明,如下(对学生不要求):
设P(x,y)在图示抛物线上,则
OP2=x2+y2=(4-2y)+y2=(y-1)2+3.
∵0≤y≤2,
∴3≤OP2≤4.
∴点P在半圆x2+y2=3、x2+y2=4所夹的圆环内,以及点P为内圆周点(
 ,1)与外圆周点A、B、C.
,1)与外圆周点A、B、C.∴半圆⊙O的面积大于图示阴影部分的面积.

由于内半圆的面积为
 S⊙O-
S⊙O- ,
,∴
 <S<2π.
<S<2π.如果学生能得出此结论,可在上面结论基础上,加(4分).
方法二:
由题意,可知这段图象与x轴的交点为A(-2,0)、B(2,0),与y轴的交点为C(0,2).(2分)
显然,这段图象在图示半径为
 、2的两个半圆所夹的圆环内,以及过内半圆上点
、2的两个半圆所夹的圆环内,以及过内半圆上点P(
 ,1)与半外圆上点A、B、C.(5分)
,1)与半外圆上点A、B、C.(5分)∴S在图示两个半圆面积之间.(7分)
即
 π•(
π•( )2<S<
)2<S< π•22.(9分)
π•22.(9分)∴
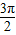 <S<2π.(10分)
<S<2π.(10分)点评:此题考查了同学们的估算能力,用不同的图形为标准可得到不同的取值范围,有利于培养同学们的创新思维能力.当以后学习了积分,可直接求的阴影部分的准确值.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
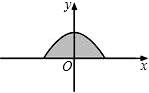 (附加题:如果你的全卷得分不足150分,则本题的得分记入总分,但记入总分后全卷得分不得超过150分,超过按150分算.)
(附加题:如果你的全卷得分不足150分,则本题的得分记入总分,但记入总分后全卷得分不得超过150分,超过按150分算.) x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.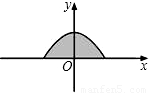
 x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
 x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.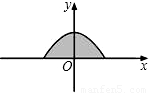
 x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.