题目内容
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-| 1 |
| 2 |
| A、a<0 | ||||
B、当x<-
| ||||
| C、a+b+c>0 | ||||
D、当x=-
|
考点:二次函数图象与系数的关系,二次函数的性质
专题:
分析:根据抛物线开口方向可对A进行判断;根据当抛物线开口向上,在对称轴左侧y随x的增大而减小的性质可对B进行判断;观察函数图象得到当x=1时,y<0,则可对C进行判断;先根据对称轴方程得到a=b,再由抛物线开口向上,函数有最小值=
,然后约分后即可对D进行判断.
| 4ac-b2 |
| 4a |
解答:解:A、抛物线开口向上,则a>0,所以A选项错误;
B、抛物线开口向上,对称轴为直线x=-
,则x<-
时,y随x的增大而减小,所以B选项错误;
C、当x=1时,y<0,即a+b+c<0,所以C选项错误;
D、对称轴为直线x=-
=-
,则a=b,因为抛物线开口向上,所以函数有最小值=
=
,所以D选项正确.
故选D.
B、抛物线开口向上,对称轴为直线x=-
| 1 |
| 2 |
| 1 |
| 2 |
C、当x=1时,y<0,即a+b+c<0,所以C选项错误;
D、对称轴为直线x=-
| b |
| 2a |
| 1 |
| 2 |
| 4ac-b2 |
| 4a |
| 4c-b |
| 4 |
故选D.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
,函数有最小值
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.也考查了二次函数的性质.
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
如图中角的表示方法正确的个数有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
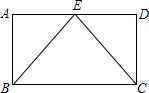 如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,
如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,①△ABE≌△DCE;②△ABE和△DCE都是等腰直角三角形;③AE=DE;④△BCE是等边三角形,
以上结论正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
方程x2-3x=0的解是( )
| A、x=3 |
| B、x1=0,x2=3 |
| C、x1=0,x2=-3 |
| D、x1=1,x2=-3 |
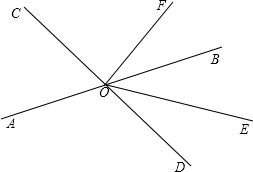 如图,直线AB、CD相交于点O,OE平分∠BOD.
如图,直线AB、CD相交于点O,OE平分∠BOD.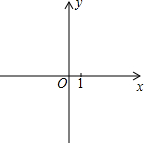 已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数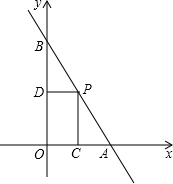 如图,直线y=-2x+8交x轴于A,交Y轴于B,点P在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S.
如图,直线y=-2x+8交x轴于A,交Y轴于B,点P在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S. 在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标.
在平面直角坐标系xOy中,A点的坐标为(3,4),将OA绕原点O顺时针旋转90°得到OA′,求点A′的坐标. 如图,DE是△ABC的中位线,M、N分别是BD、CE的中点,BC=8,则MN=
如图,DE是△ABC的中位线,M、N分别是BD、CE的中点,BC=8,则MN=