题目内容
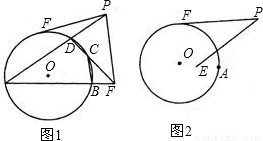
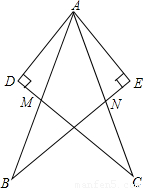
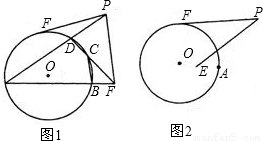
(2002•荆门)已知:如图,PF是⊙O的切线,PE=PF,A是⊙O上一点,直线AE、AP分别交⊙O于B、D,直线DE交⊙O于C,连接BC,(1)求证:PE∥BC;
(2)将PE绕点P顺时针旋转,使点E移到圆内,并在⊙O上另选一点A,如图2.其他条件不变,在图2中画出完整的图形.此时PE与BC是否仍然平行?证明你的结论.
【答案】分析:(1)根据切割线定理,PE=PF得出PE:PD=PA:PE,∠APE=∠APE得出△EPD∽△APE,再根据外接圆的性质得出内错角相等,得出PE∥BC.
(2)证明△EPD∽△APE,通过∠B=∠D得出内错角相等PE∥BC.
解答:(1)证明:∵PF与⊙O相切,
∴PF2=PD•PA.
∵PE=PF,
∴PE2=PD•PA.
∴PE:PD=PA:PE.
∵∠APE=∠APE,
∴△EPD∽△APE.
∴∠PED=∠A.
∵∠ECB=∠A,
∴∠PED=∠ECB.
∴PE∥BC.
(2)解:PE与BC仍然平行.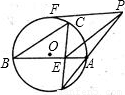
证明:画图如图,
∵△EPD∽△APE,
∴∠PEA=∠D.
∵∠B=∠D,
∴∠PEA=∠B.
∴PE∥BC.
点评:此题考查圆的切割线定理,外接圆的性质,相似三角形的判定和性质及平行线的判定.
(2)证明△EPD∽△APE,通过∠B=∠D得出内错角相等PE∥BC.
解答:(1)证明:∵PF与⊙O相切,
∴PF2=PD•PA.
∵PE=PF,
∴PE2=PD•PA.
∴PE:PD=PA:PE.
∵∠APE=∠APE,
∴△EPD∽△APE.
∴∠PED=∠A.
∵∠ECB=∠A,
∴∠PED=∠ECB.
∴PE∥BC.
(2)解:PE与BC仍然平行.

证明:画图如图,
∵△EPD∽△APE,
∴∠PEA=∠D.
∵∠B=∠D,
∴∠PEA=∠B.
∴PE∥BC.
点评:此题考查圆的切割线定理,外接圆的性质,相似三角形的判定和性质及平行线的判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目