题目内容
【题目】为测量大楼
的高度，从距离大楼底部
30米处的
，有一条陡坡公路，车辆从沿坡度
，坡面长13米的斜坡到达
后，观测到大楼的顶端
的仰角为30°，则大楼的高度为（ ）米．
（精确到0.1米，
，
）
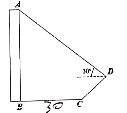
A.26.0B.29.2C.31.1D.32.2
【答案】B
【解析】
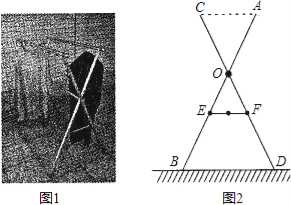
过点D作DF⊥AB与点F，过点C作CE⊥DF与点E，通过解直角三角形可求出CE、DE、AF的长，再由AB=AF+BF即可求出结论．
解：过点D作DF⊥AB与点F，过点C作CE⊥DF与点E，如图所示．
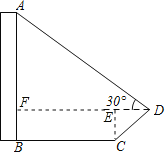
∵CD的坡度i=1：2.4，CD=13，
∴设CE=x，则DE=2.4x，
∴CD=
x=13，
∴x=5，
∴CE=5米，DE=12米．
在Rt△ADF中，∠ADF=30°，DF=DE+EF=42，
∴AF=DFtan∠ADF≈24.2米，
∴AB=AF+BF=29.2米．
故选：B．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】参照学习函数的过程与方法，探究函数
的图象与性质列表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值为纵坐标，描出相应的点，如图所示：
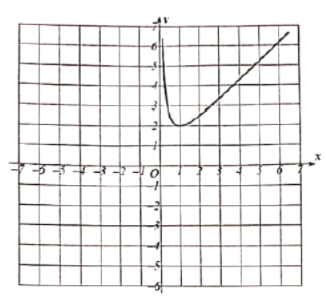
（1）请补全函数图象：
（2）观察图象并分析表格，回答下列问题：
①当
时，y随x的增大而_________；（填“增大”或“减小”）
②图象关于点__________中心对称．（填点的坐标）
③当
时，
的最小值是_________．
（3）结合函数图象，当
时，求x的取值范围．
