题目内容
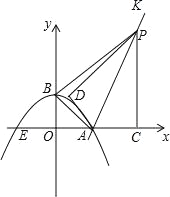
【题目】已知:如图,抛物线y=ax2+bx+2与x轴交于点A(4,0)、E(-2,0)两点,连结AB,过点A作直线AK⊥AB,动点P从A点出发以每秒![]() 个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
(1)求抛物线的解析式;
(2)当点D在△ABP的内部时,△ABP与△ADP不重叠部分的面积为S,求S与t之间的函数关系式,并直接写出t的取值范围;
(3)若线段AC的长是线段BP长的![]() ,请直接写出此时t的值;
,请直接写出此时t的值;
(4)是否存在这样的时刻,使动点D到点O的距离最小?若存在请直接写出这个最小距离;若不存在,说明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+2,(2)S=-t2+5t(0<t<4)(3)t=
x+2,(2)S=-t2+5t(0<t<4)(3)t=![]() ;(4)
;(4)![]() .
.
【解析】
试题分析:(1)用待定系数法求出抛物线解析式;
(2)先根据点D在△APB内部,求出t的范围,然后用△APB减去△APC面积求出不重叠的部分面积;
(3)根据两点间的距离公式表示出BP,根据条件建立方程,求出时间;
(4)先判断出点D到点O的距离最小时的位置,然后用三角函数和勾股定理计算.
试题解析:(1)将A,B,E三点代入抛物线解析式中,得
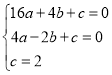 ,∴
,∴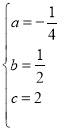
∴y=-![]() x2+
x2+![]() x+2,
x+2,
(2)∵A(4,0),B(0,2)
∴直线AB解析式为y=-![]() x+2,
x+2,
∵AB⊥AK,
∴直线AK解析式为y=2x+8,
∴tan∠PAC=![]() =2,
=2,
∵AP=![]() t,
t,
∴AC=t,PC=2t,
∵D在△ABP内部,
∴∠APB>∠APC,
∴tan∠APB>tan∠APC,
∴![]() ,
,
∴![]() ,
,
∴t<4,
∴0<t<4,
∴S=S△APB-S△APD
=S△APB-S△APC
=![]() ×AB×AP-
×AB×AP-![]() ×AC×PC
×AC×PC
=![]() ×2
×2![]() ×
×![]() t-
t-![]() ×t×2t
×t×2t
=-t2+5t(0<t<4)
(3)∵P(t+4,2t),
∴BP=![]() ,
,
∵线段AC的长是线段BP长的![]() ,
,
∴t=![]() ,
,
∴t=-![]() (舍)t=
(舍)t=![]()
(4)要使点D到O的距离最小,则有点D在OP上,此时记作D1
在Rt△OCP中,tan∠POC=![]() ,
,
在Rt△OCP中,tan∠AOC=![]() ,
,
∴![]() ,
,
∴OD1=![]() ,
,
根据勾股定理得,OD12+AD12=OA2,
∴(![]() )2+t2=16,
)2+t2=16,
∴t=-4(舍)t=![]() ,
,
∴AD1=![]() =
=![]() .
.
