题目内容
为使x2-7x+b在整数范围内可以分解因式，则b可能取的值为
此题答案不唯一，如6等
此题答案不唯一，如6等
．分析：利用十字相乘法分解因式的知识，可知-7是两个整数的和，b是此两个整数的积，故此题答案不唯一，如-7=（-1）+（-6），此时b=6．
解答：解：此题答案不唯一，如-7=（-1）+（-6），
则x2-7x+b=（x-1）（x-6）=x2-7x+6，
此时b=6．
故答案为：此题答案不唯一，如6等．
则x2-7x+b=（x-1）（x-6）=x2-7x+6，
此时b=6．
故答案为：此题答案不唯一，如6等．
点评：此题考查了十字相乘法分解因式的知识．此题属于开放题，答案不唯一，注意-7是两个整数的和，b是此两个整数的积．
练习册系列答案
相关题目
的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．
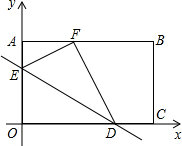如图，将矩形OABC放置在平面直角坐标系中，点D在边0C上，点E在边OA上，把矩形沿直线DE翻折，使点O落在边AB上的点F处，且tan∠BFD=
如图，?ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．
已知：线段OA、OB（OA＜OB）的长是一元二次方程x2-7x+12=0的两个根．