题目内容
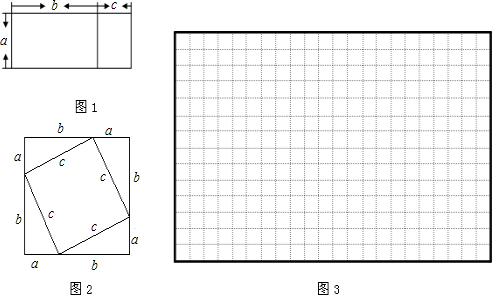
通过前面的学习,我们知道利用面积的不同表示方法可以写出一个代数恒等式,比如图1的图形,我们可以把它看成长为(b+c),宽为a的长方形,则图形的面积为______,我们也可以把它看成是两个长方形组成的图形,则此时,它的面积可以表示为______,所以我们可以得到等式______
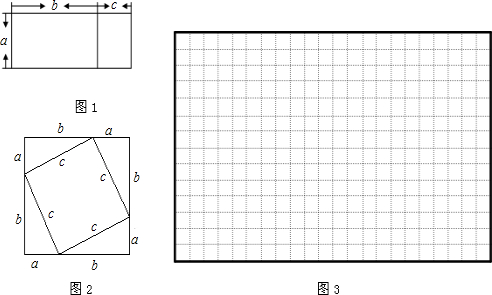
(1)图2的图形蕴涵着一个著名定理,请你运用面积不同的表达方式推导出这个定理.
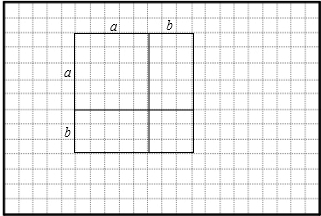
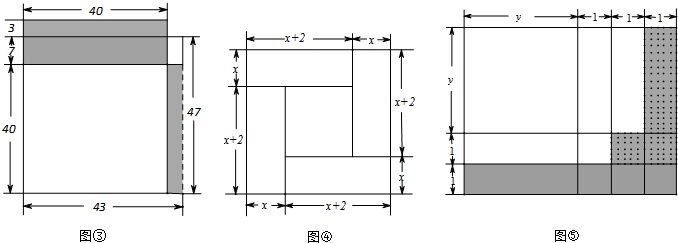
(2)在图3中,试画一个几何图形,使它的面积能够表示:(a+b)2=a2+2ab+b2(把图形作在方格中)

(1)图2的图形蕴涵着一个著名定理,请你运用面积不同的表达方式推导出这个定理.
(2)在图3中,试画一个几何图形,使它的面积能够表示:(a+b)2=a2+2ab+b2(把图形作在方格中)
a(b+c),ab+ac,a(b+c)=ab+ac;
(1)证明:正方形的面积:(a+b)2,
正方形的面积也可以表示为:4×
| 1 |
| 2 |
所以,4×
| 1 |
| 2 |
即c2=a2+b2;
(2)如图所示,正方形的面积可以表示为:(a+b)2,
也可以表示为a2+2ab+b2,
所以,(a+b)2=a2+2ab+b2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





 ,宽为
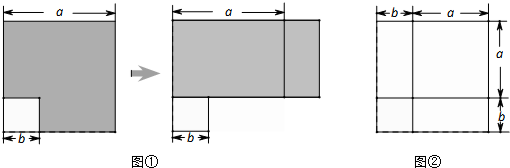
,宽为 的矩形,构造图④
的矩形,构造图④
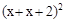 或四个长
或四个长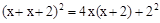




 的解
的解 与
与 的大小关系(其中
的大小关系(其中 )?
)? ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割

 ,
, ,即
,即 ,
,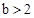 时,表示
时,表示 与
与 的大小关系
的大小关系 ,
,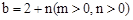 ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)