Question

8、已知梯形的上、下底分别为6和8，一腰长为7，则另一腰a的取值范围是（　　）

A、6＜a＜8

B、5＜a＜9

C、a＜7

D、a＞7

Answer 1

分析：本题可画出图形，然后根据三角形的三边关系：两边之差＜第三边，两边之和＞第三边来解题．

解答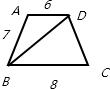：解：如图：连接BD，
则：7-6＜BD＜7+6，
即1＜BD＜13，
则|BC-BD|＜CD＜BC+BD，
因为5＜|BC-BD|＜7，
9＜BC+BD＜14，
∴|BC-BD|＜7＜CD＜9＜BC+BD．
法二、作辅助线，平移一腰，则构造了一个三角形．
三边是两个腰、梯形的两底之差（8-6=2）．
再根据三角形的三边关系7-2＜a＜7+2，
即5＜a＜9．
故选B．

点评：本题考查的是三角形的三边关系和梯形的性质，解此类题目时常常是画出图形、作出辅助线，然后根据三角形的三边关系：两边之差＜第三边，两边之和＞第三边来解题．