题目内容
 如图,半径为1的⊙M经过直角坐标系的原点O,且分别与x轴正半轴、y轴正半轴交于点A、B,∠OMA=60°,过点B的切线交x轴负半轴于点C,抛物线过点A、B、C.
如图,半径为1的⊙M经过直角坐标系的原点O,且分别与x轴正半轴、y轴正半轴交于点A、B,∠OMA=60°,过点B的切线交x轴负半轴于点C,抛物线过点A、B、C.(1)求点A、B的坐标;
(2)求抛物线的函数关系式;
(3)若点D为抛物线对称轴上的一个动点,问是否存在这样的点D,使得△BCD是等腰三角形?若存在,求出符合条件的点D的坐标;若不存在,请说明理由.
分析:(1)由题意可直接得出点A、B的坐标为A(1,0),B(0,
);
(2)再根据BC是切线,可求出BC的长,即得出点C的坐标,由待定系数法求出抛物线的解析式;
(3)先假设存在,看能否求出符合条件的点D即可.
| 3 |
(2)再根据BC是切线,可求出BC的长,即得出点C的坐标,由待定系数法求出抛物线的解析式;
(3)先假设存在,看能否求出符合条件的点D即可.
解答:解:(1)∵MO=MA=1,∠OMA=60°,
∴∠ABO=30°,
∴OB=
,
∴A(1,0),B(0,
);
(2)∵BC是切线,
∴∠ABC=90°,
∴∠ACB=30°,
∴AC=4,
∴C(-3,0),
设抛物线的解析式为y=ax2+bx+c,将点A、B、C代入得,
,
解得

∴抛物线的解析式为y=-
x2-
x+
;
(3)设在对称轴上存在点D,使△BCD是等腰三角形,
对称轴为直线x=-1,设点D(-1,m),
分3种情况讨论:①BC=BD;
=2
,
解得m=±
+
;
②BC=CD;
=2
,解得m=±2
;
③BD=CD;
=
,解得:m=0,
∴符合条件的点D的坐标为,(-1,
+
),(-1,-
+
),(-1,2
),(-1,-2
),(-1,0).
∴∠ABO=30°,
∴OB=
| 3 |
∴A(1,0),B(0,
| 3 |
(2)∵BC是切线,
∴∠ABC=90°,
∴∠ACB=30°,
∴AC=4,
∴C(-3,0),
设抛物线的解析式为y=ax2+bx+c,将点A、B、C代入得,
|
解得
|

∴抛物线的解析式为y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(3)设在对称轴上存在点D,使△BCD是等腰三角形,
对称轴为直线x=-1,设点D(-1,m),
分3种情况讨论:①BC=BD;
1+(m-
|
| 3 |
解得m=±
| 11 |
| 3 |
②BC=CD;
| 4+m2 |
| 3 |
| 2 |
③BD=CD;
| 4+m2 |
1+(m-
|
∴符合条件的点D的坐标为,(-1,
| 11 |
| 3 |
| 11 |
| 3 |
| 2 |
| 2 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和等腰三角形判定等知识点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,
如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,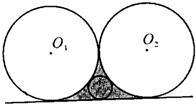 12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于
12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°. 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为