题目内容
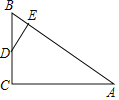
【题目】如图,二次函数![]() 的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.

(1)求二次函数的解析式;
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并说明理由;
(3)若点M在x轴上,点P在抛物线上,是否存在以点A,E,M,P为顶点且以AE为一边的平行四边形?若存在,请求出所有满足要求的点P的坐标;若不存在,请说明理由.
【答案】(1)y=x22x3.(2)四边形EFCD是正方形,理由见解析;P点坐标为(1+![]() ,3)或(1
,3)或(1![]() ,3)或(0,3)
,3)或(0,3)
【解析】
(1)根据抛物线的对称轴为直线x=1得![]() ,求出b,再根据C(0,-3)求出c=-3即可;
,求出b,再根据C(0,-3)求出c=-3即可;
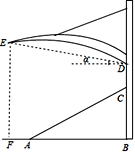
(2)结论四边形EFCD是正方形.如图1中,连接CE与DF交于点K.求出E、F、D、C四点坐标,只要证明DF⊥CE,DF=CE,KC=KE,KF=KD即可证明.
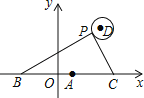
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.根据点P的纵坐标为3或3,即可解决问题.
(1)∵二次函数![]() 的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
∴![]()
∴b=-2,
∵C(0,-3)
∴c=-3.
∴抛物线的解析式为y=x22x3.
(2)结论:四边形EFCD是正方形.
理由:如图1中,连接CE与DF交于点K.

∵y=(x1)24,
∴顶点D(1,4),
∵C、E关于对称轴对称,C(0,3),
∴E(2,3),
∵A(1,0),
设直线AE的解析式为y=kx+b,则
![]() ,解得
,解得![]() ,
,
∴直线AE的解析式为y=x1.
∴F(1,2),
∴CK=EK=1,FK=DK=1,
∴四边形EFCD是平行四边形,
又∵CE⊥DF,CE=DF,
∴四边形EFCD是正方形.
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.

由题意点P的纵坐标为3或3,
当y=3时,x22x3=3,解得x=1±![]() ,
,
可得P1(1+![]() ,2),P2(1
,2),P2(1![]() ,
,
当y=2时,x=0,可得P3(0,3),
综上所述当P点坐标为(1+![]() ,3)或(1
,3)或(1![]() ,3)或(0,3)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
,3)或(0,3)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.