ĢāÄæÄŚČŻ
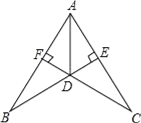
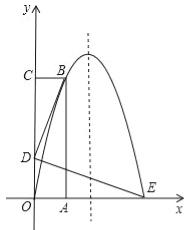
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖ×ų±źŌµć£¬Å×ĪļĻßy=ax2+2xa+c¾¹żA£Ø©4£¬0£©£¬B£Ø0£¬4£©Į½µć£¬ÓėxÖį½»ÓŚĮķŅ»µćC£¬Ö±Ļßy=x+5ÓėxÖį½»ÓŚµćD£¬ÓėyÖį½»ÓŚµćE£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćPŹĒµŚ¶žĻóĻŽÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓEP£¬¹żµćE×÷EPµÄ“¹Ļßl£¬ŌŚlÉĻ½ŲČ”Ļ߶ĪEF£¬Ź¹EF=EP£¬ĒŅµćFŌŚµŚŅ»ĻóĻŽ£¬¹żµćF×÷FM”ĶxÖįÓŚµćM£¬ÉčµćPµÄŗį×ų±źĪŖt£¬Ļ߶ĪFMµÄ³¤¶ČĪŖd£¬ĒódÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£Ø²»ŅŖĒ󊓳ö×Ō±äĮætµÄȔֵ·¶Ī§£©£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµćE×÷EH”ĶED½»MFµÄŃÓ³¤ĻßÓŚµćH£¬Į¬½ÓDH£¬µćGĪŖDHµÄÖŠµć£¬µ±Ö±ĻßPG¾¹żACµÄÖŠµćQŹ±£¬ĒóµćFµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©d=5+t£»£Ø3£©F
£»£Ø2£©d=5+t£»£Ø3£©F![]() .
.
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©Ö±½Ó°ŃA”¢B×ų±ź“śČėĒó³öa”¢cµĆÖµ¼“æÉ£»£Ø2£©·Ö±š¹żP”¢FĻņyÖį×÷“¹Ļߣ¬“¹×ć·Ö±šĪŖA”䔢B”䣬¹żP×÷PN”ĶxÖį£¬“¹×ćĪŖN£¬Ņ×Ö¤”÷PEA”ä”Õ”÷EFB”䣬æÉµĆ³öd=FM=OE©EB”䣬ŌŁ“śČėæÉĒóµĆ½āĪöŹ½£»£Ø3£©ĻČĒóµĆF”¢HµÄ×ų±ź£¬·¢ĻÖµćPŗĶµćHµÄׯ×ų±źĻąµČ£¬ŌņPHÓėxÖįĘ½ŠŠ£¬øł¾ŻĘ½ŠŠĻß½ŲĻ߶Ī³É±ČĄż¶ØĄķæɵĆGŅ²ŹĒPQµÄÖŠµć£¬ÓÉ“Ė±ķŹ¾³öµćGµÄ×ų±ź²¢ĮŠŹ½£¬Ēó³ötµÄÖµ²¢Č”Éį£¬¼ĘĖć³öµćFµÄ×ų±ź£®
ŹŌĢā½āĪö£ŗ£Ø1£©ÓÉĢāŅāµĆ![]() £¬½āµĆ
£¬½āµĆ £¬”ąÅ×ĪļĻß½āĪöŹ½ĪŖ
£¬”ąÅ×ĪļĻß½āĪöŹ½ĪŖ![]() £»£Ø2£©·Ö±š¹żP”¢FĻņyÖį×÷“¹Ļߣ¬“¹×ć·Ö±šĪŖA”䔢B”䣬¹żP×÷PN”ĶxÖį£¬“¹×ćĪŖN£¬µ±x=0Ź±£¬y=5£¬”ąE£Ø0£¬5£©£¬”ąOE=5£¬”ß”ĻPEO+”ĻOEF=90”ć£¬”ĻPEO+”ĻEPA”ä=90”ć£¬”ą”ĻEPA”ä=”ĻOEF£¬”ßPE=EF£¬”ĻEA”äP=”ĻEB”äF=90”ć£¬”ą”÷PEA”ä”Õ”÷EFB”䣬”ąPA”ä=EB”ä=©t£¬”ąd=FM=OB”ä=OE©EB”ä=5©£Ø©t£©=5+t£»
£»£Ø2£©·Ö±š¹żP”¢FĻņyÖį×÷“¹Ļߣ¬“¹×ć·Ö±šĪŖA”䔢B”䣬¹żP×÷PN”ĶxÖį£¬“¹×ćĪŖN£¬µ±x=0Ź±£¬y=5£¬”ąE£Ø0£¬5£©£¬”ąOE=5£¬”ß”ĻPEO+”ĻOEF=90”ć£¬”ĻPEO+”ĻEPA”ä=90”ć£¬”ą”ĻEPA”ä=”ĻOEF£¬”ßPE=EF£¬”ĻEA”äP=”ĻEB”äF=90”ć£¬”ą”÷PEA”ä”Õ”÷EFB”䣬”ąPA”ä=EB”ä=©t£¬”ąd=FM=OB”ä=OE©EB”ä=5©£Ø©t£©=5+t£»

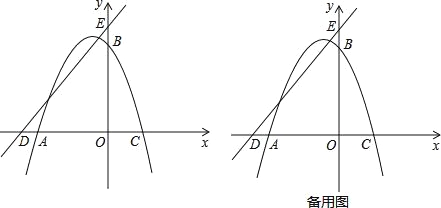
£Ø3£©ČēĶ¼£¬ÓÉÖ±ĻßDEµÄ½āĪöŹ½ĪŖ£ŗy=x+5£¬”ßEH”ĶED£¬”ąÖ±ĻßEHµÄ½āĪöŹ½ĪŖ£ŗy=©x+5£¬
”ąFB”ä=A”äE=5©£Ø©![]() t2©t+4£©=
t2©t+4£©=![]() t2+t+1£¬”ąF£Ø
t2+t+1£¬”ąF£Ø![]() t2+t+1£¬5+t£©£¬”ąµćHµÄŗį×ų±źĪŖ£ŗ
t2+t+1£¬5+t£©£¬”ąµćHµÄŗį×ų±źĪŖ£ŗ![]() t2+t+1£¬
t2+t+1£¬
y=©![]() t2©t©1+5=©
t2©t©1+5=©![]() t2©t+4£¬”ąH£Ø
t2©t+4£¬”ąH£Ø![]() t2+t+1£¬©
t2+t+1£¬©![]() t2©t+4£©£¬”ßGŹĒDHµÄÖŠµć£¬”ąG£Ø
t2©t+4£©£¬”ßGŹĒDHµÄÖŠµć£¬”ąG£Ø £©£¬¼“G£Ø
£©£¬¼“G£Ø![]() t2+
t2+![]() t©2£¬©
t©2£¬©![]() t2©
t2©![]() t+2£©£¬”ąPH”ĪxÖį£¬”ßDG=GH£¬”ąPG=GQ£¬
t+2£©£¬”ąPH”ĪxÖį£¬”ßDG=GH£¬”ąPG=GQ£¬
”ą![]() £¬½āµĆt=
£¬½āµĆt=![]() £¬”ßPŌŚµŚ¶žĻóĻŽ£¬”ąt£¼0£¬”ąt=
£¬”ßPŌŚµŚ¶žĻóĻŽ£¬”ąt£¼0£¬”ąt=![]() £¬”ąF£Ø
£¬”ąF£Ø![]() £©£®
£©£®

 Š”Ģģ²ÅæĪŹ±×÷ŅµĻµĮŠ“š°ø
Š”Ģģ²ÅæĪŹ±×÷ŅµĻµĮŠ“š°ø Ņ»æĪĖÄĮ·ĻµĮŠ“š°ø
Ņ»æĪĖÄĮ·ĻµĮŠ“š°ø »ĘøŌŠ”דŌŖĀś·Ö³å“ĢĪ¢²āŃéĻµĮŠ“š°ø
»ĘøŌŠ”דŌŖĀś·Ö³å“ĢĪ¢²āŃéĻµĮŠ“š°ø ŠĀøؽĢµ¼Ń§ĻµĮŠ“š°ø
ŠĀøؽĢµ¼Ń§ĻµĮŠ“š°ø Ńō¹āĶ¬Ń§Ņ»ĻßĆūŹ¦Č«ÓÅŗĆ¾ķĻµĮŠ“š°ø
Ńō¹āĶ¬Ń§Ņ»ĻßĆūŹ¦Č«ÓÅŗĆ¾ķĻµĮŠ“š°ø”¾ĢāÄæ”æ¼ĘĖć£ŗ
£Ø1£©©66”Į4+£Ø©2.5£©”Ā£Ø©0.1£©
£Ø2£©£Ø©2£©3+£Ø©3£©”Į[£Ø©4£©2+2]+£Ø©3£©2”Ā£Ø©2£©
”¾ĢāÄæ”æ2017Äź¹śĒģ½ŚĘŚ¼ä£¬ÄĻÄž¶ÆĪļŌ°ŌŚ7Ģģ¼ŁĘŚÖŠĆæĢģ½Ó“żÓĪæĶµÄČĖŹżÓėĒ°Ņ»ĢģĻą±ČµÄ±ä»ÆĒéæö£ØÕżŹż±ķŹ¾±ČĒ°Ņ»Ģģ¶ąµÄČĖŹż,øŗŹż±ķŹ¾±ČĒ°Ņ»ĢģÉŁµÄČĖŹż£©ČēĻĀ±ķ£ŗ
ČÕĘŚ | 1ČÕ | 2ČÕ | 3ČÕ | 4ČÕ | 5ČÕ | 6ČÕ | 7ČÕ |
ČĖŹż±ä»Æ/ĶņČĖ | +1.7 | +0.6 | +0.3 | -0.3 | -0.6 | +0.2 | -1.1 |
(1) ĒėÅŠ¶ĻĘßĢģÄŚÓĪæĶČĖŹż×ī¶ąµÄŹĒÄÄĢģ?×īÉŁµÄŹĒÄÄĢģ?ĖüĆĒĻą²ī¶ąÉŁĶņČĖ?
(2) Čō9ŌĀ30ČÕµÄÓĪæĶČĖŹżĪŖ3ĶņČĖ,ĒóÕā7ĢģµÄÓĪæĶ×ÜČĖŹżŹĒ¶ąÉŁĶņČĖ?