题目内容
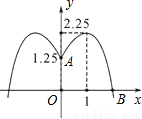
 某学校要在圆形水池的中心点O处安装水管OA=1.25米,要建音乐喷泉,其水流路径呈抛物线型(如图),且在离O点1米处水喷得最高2.25米,要使水流不溅到池外,水池的半径应不少于多少米?
某学校要在圆形水池的中心点O处安装水管OA=1.25米,要建音乐喷泉,其水流路径呈抛物线型(如图),且在离O点1米处水喷得最高2.25米,要使水流不溅到池外,水池的半径应不少于多少米?
解:∵如图可知:抛物线的顶点坐标为(1,2.25),
∴设y=a(x-1)2+2.25,
∵抛物线过(0,1.25),
代入y=a(x-1)2+2.25,
得:a=-1.
则函数的解析式都是y=-(x-1)2+2.25,
当y=0时,-(x-1)2+2.25=0,解得:x=2.5或-0.5(舍去).
∴要使水流不溅到池外,水池的半径应不少于2.5米.
分析:要使水流不溅到池外,则表现在坐标系上为半径即使抛物线与x轴的交点的最小值,以右半边的抛物线为例,由顶点坐标(1,2.25),与y轴的交点(0,1.25)可求出此抛物线的解析式,再求其与x轴的交点即可.
点评:本题考查的二次函数在实际生活中的应用,比较简单,注意数形结合.
∴设y=a(x-1)2+2.25,
∵抛物线过(0,1.25),
代入y=a(x-1)2+2.25,
得:a=-1.
则函数的解析式都是y=-(x-1)2+2.25,
当y=0时,-(x-1)2+2.25=0,解得:x=2.5或-0.5(舍去).
∴要使水流不溅到池外,水池的半径应不少于2.5米.
分析:要使水流不溅到池外,则表现在坐标系上为半径即使抛物线与x轴的交点的最小值,以右半边的抛物线为例,由顶点坐标(1,2.25),与y轴的交点(0,1.25)可求出此抛物线的解析式,再求其与x轴的交点即可.
点评:本题考查的二次函数在实际生活中的应用,比较简单,注意数形结合.

练习册系列答案
相关题目
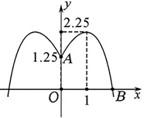 19、某学校要在圆形水池的中心点O处安装水管OA=1.25米,要建音乐喷泉,其水流路径呈抛物线型(如图),且在离O点1米处水喷得最高2.25米,要使水流不溅到池外,水池的半径应不少于多少米?
19、某学校要在圆形水池的中心点O处安装水管OA=1.25米,要建音乐喷泉,其水流路径呈抛物线型(如图),且在离O点1米处水喷得最高2.25米,要使水流不溅到池外,水池的半径应不少于多少米?