题目内容
三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?
(3)探究:腰长为2的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?为什么?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?

【答案】分析:(1)对角线平分每一对角的四边形都可以,如菱形、正方形;
(2)对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等;
(3)根据O到AB的距离等于O到DE的距离,即可得到答案;
(4)由勾股定理求出AB=2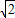 ,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2
,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2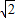 ,代入即可求出答案.
,代入即可求出答案.
解答:(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
理由是根据角平分线的性质得到:O到AB的距离等于O到DE的距离,在△ABC内有无数条,如图:具备DE∥AB即可.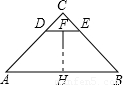
(4)
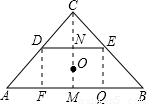
解:等腰直角三角形ACB,AC=BC=2,由勾股定理得:AB=2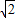 ,
,
过D作DF⊥AB于F,过E作EQ⊥AB于Q,
∴DF∥EQ,
∵DE∥AB,
∴四边形DEQF是平行四边形,
∴DE=FQ,DF=EQ,
∵∠A=∠B=45°,
∴AF=DF,
同理BQ=QE,
设DE=x,AB=2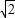 ,过C作CM⊥BC,交DE与N点,
,过C作CM⊥BC,交DE与N点,
由AB=AC,根据三线合一可得CM=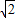 ,
,
由三角形的面积有两种求法,S= AC•BC=
AC•BC= (AC+BC+AB)•OM,
(AC+BC+AB)•OM,
即4=(2+2+2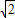 )×OM,解得:OM=2-
)×OM,解得:OM=2-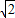 ,
,
∴NM=2OM=4-2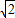 ,CN=
,CN=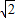 -(4-2
-(4-2 )=3
)=3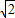 -4,
-4,
又△CDE∽△CAB,
∴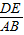 =
=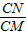 ,即
,即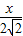 =
=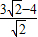 ,
,
解得:x=6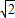 -8,
-8,
则DE=6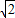 -8.
-8.
点评:本题主要考查对平行四边形的性质和判定,勾股定理,角平分线的性质,三角形的内切圆与内心,等腰题型的性质等知识点的理解和掌握,此题是一个拔高的题目,有一定难度.
(2)对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等;
(3)根据O到AB的距离等于O到DE的距离,即可得到答案;
(4)由勾股定理求出AB=2
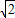 ,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2
,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2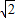 ,代入即可求出答案.
,代入即可求出答案.解答:(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
理由是根据角平分线的性质得到:O到AB的距离等于O到DE的距离,在△ABC内有无数条,如图:具备DE∥AB即可.

(4)

解:等腰直角三角形ACB,AC=BC=2,由勾股定理得:AB=2
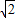 ,
,过D作DF⊥AB于F,过E作EQ⊥AB于Q,
∴DF∥EQ,
∵DE∥AB,
∴四边形DEQF是平行四边形,
∴DE=FQ,DF=EQ,
∵∠A=∠B=45°,
∴AF=DF,
同理BQ=QE,
设DE=x,AB=2
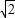 ,过C作CM⊥BC,交DE与N点,
,过C作CM⊥BC,交DE与N点,由AB=AC,根据三线合一可得CM=
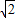 ,
,由三角形的面积有两种求法,S=
 AC•BC=
AC•BC= (AC+BC+AB)•OM,
(AC+BC+AB)•OM,即4=(2+2+2
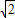 )×OM,解得:OM=2-
)×OM,解得:OM=2-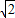 ,
,∴NM=2OM=4-2
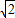 ,CN=
,CN=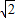 -(4-2
-(4-2 )=3
)=3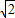 -4,
-4,又△CDE∽△CAB,
∴
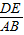 =
=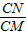 ,即
,即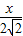 =
=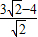 ,
,解得:x=6
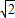 -8,
-8,则DE=6
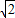 -8.
-8.点评:本题主要考查对平行四边形的性质和判定,勾股定理,角平分线的性质,三角形的内切圆与内心,等腰题型的性质等知识点的理解和掌握,此题是一个拔高的题目,有一定难度.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目



