题目内容
(2008•遵义)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.(1)若该超市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案.
【答案】分析:依据等量关系“购进甲、乙两种商品共80件,恰好用去1600元”列方程求得甲、乙两种商品的件数,然后依据不等关系“总利润不少于600元,但又不超过610元”列出不等式组,通过解不等式组来确定“进货方案”.
解答:解:(1)设甲商品进了a件,则乙种商品进了(80-a)件,依题意得:
10a+(80-a)×30=1600,
解得:a=40,
即甲种商品进了40件,乙种商品进了80-40=40件.
(2)设购买甲种商品为x件,则购买乙种商品为(80-x)件,依题意可得:
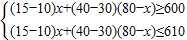 ,
,
解得:38≤x≤40.
即有三种方案,分别为甲38件,乙42件或甲39件,乙41件或甲40件,乙40件.
点评:利用方程和不等式组解答的“方案设计题”是中考的热点考题,其关键点就是通过解不等式组求得某一个未知量的整数解,从而确定“设计方案”.
解答:解:(1)设甲商品进了a件,则乙种商品进了(80-a)件,依题意得:
10a+(80-a)×30=1600,
解得:a=40,
即甲种商品进了40件,乙种商品进了80-40=40件.
(2)设购买甲种商品为x件,则购买乙种商品为(80-x)件,依题意可得:
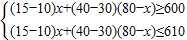 ,
,解得:38≤x≤40.
即有三种方案,分别为甲38件,乙42件或甲39件,乙41件或甲40件,乙40件.
点评:利用方程和不等式组解答的“方案设计题”是中考的热点考题,其关键点就是通过解不等式组求得某一个未知量的整数解,从而确定“设计方案”.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
(2008•遵义)某学校在开展“节约每一滴水”的活动中,从七年级的180名同学中任选出十名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:请你估计这180名同学的家庭一个月节约用水的总量大约是( )
A.180吨
B.200吨
C.216吨
D.360吨
| 节水量(单位:吨) | 0.5 | 1 | 1.5 | 2 |
| 同学数(人) | 2 | 3 | 4 | 1 |
A.180吨
B.200吨
C.216吨
D.360吨