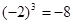题目内容
如图所示：有理数a、b、c在数轴上分别对应点A、B、C，点O为原点，化简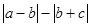
= 
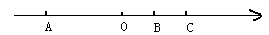
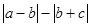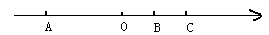
= -a-c
在数轴上找出对应的点，根据右边的数总大于左边的数可以求得a-b，b+c的符号，从而求得|a-b|-|b+c|的值．
解答：解：结合图形，根据数轴上，右边的数总大于左边的数，可得a＜0＜b＜c．
∴a-b＜0，b+c＞0，
∴|a-b|-|b+c|=b-a-b-c=-a-c；
故答案是：-a-c．
解答：解：结合图形，根据数轴上，右边的数总大于左边的数，可得a＜0＜b＜c．
∴a-b＜0，b+c＞0，
∴|a-b|-|b+c|=b-a-b-c=-a-c；
故答案是：-a-c．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
是两位数，
是一位数，若把
）
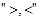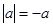； ②若
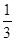）3 =-
