题目内容
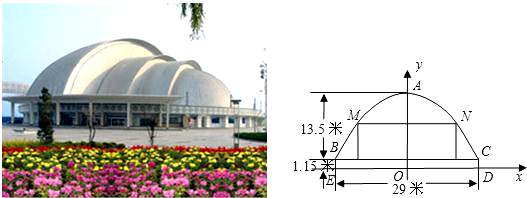
(2007•聊城)明珠大剧场座落在聊城东昌湖西岸,其上部为能够旋转的拱形钢结构,并且具有开启、闭合功能,全国独-无二,如图1.舞台顶部横剖面拱形可近似看作抛物线的一部分,其中舞台高度1.15米,台口高度13.5米,台口宽度29米,如图2.以ED所在直线为x轴,过拱顶A点且垂直于ED的直线为y轴,建立平面直角坐标系.(1)求拱形抛物线的函数关系式;
(2)舞台大幕悬挂在长度为20米的横梁MN上,其下沿恰与舞台面接触,求大幕的高度?(精确到0.01米)
【答案】分析:(1)根据抛物线在坐标系的特殊位置,对称轴是y轴时可设抛物线的关系式为y=ax2+c,由已知数据可确定顶点A坐标及点C坐标,可求抛物线解析式.
(2)已知MN的长度,就知道M,N两点的横坐标,代入抛物线解析式,求纵坐标,即为大幕的高度.
解答:解:(1)由题设可知,
OA=13.5+1.15=14.65米,OD= 米.
米.
∴A(0,14.65),C( ,1.15).
,1.15).
设拱形抛物线的关系式为y=ax2+c,
则 ,
,
解得
a=-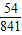 ,c=14.65.
,c=14.65.
所以,所求函数的关系式为
y=- x2+14.65.
x2+14.65.
(2)由MN=20米,设点N的坐标为(10,y),代入关系式,
得y=- ×102+14.65≈8.229.
×102+14.65≈8.229.
∴y-1.15=8.229-1.15=7.079≈7.08.
即大幕的高度约为7.08米.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
(2)已知MN的长度,就知道M,N两点的横坐标,代入抛物线解析式,求纵坐标,即为大幕的高度.
解答:解:(1)由题设可知,
OA=13.5+1.15=14.65米,OD=
 米.
米.∴A(0,14.65),C(
 ,1.15).
,1.15).设拱形抛物线的关系式为y=ax2+c,
则
 ,
,解得
a=-
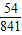 ,c=14.65.
,c=14.65.所以,所求函数的关系式为
y=-
 x2+14.65.
x2+14.65.(2)由MN=20米,设点N的坐标为(10,y),代入关系式,
得y=-
 ×102+14.65≈8.229.
×102+14.65≈8.229.∴y-1.15=8.229-1.15=7.079≈7.08.
即大幕的高度约为7.08米.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目