题目内容
如图，直线
分别与x轴、y轴交于A、B两点；直线
与AB交于点C，与过点A且平行于y轴的直线交于点D.点E从点A出发，以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）.
⑴求点C的坐标.
⑵当0<t<5时，求S与t之间的函数关系式.
⑶求⑵中S的最大值.
⑷当t>0时，直接写出点（4，
）在正方形PQMN内部时t的取值范围.
：⑴由题意，得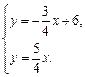
解得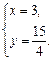
∴C（3,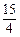
）. 3分
⑵根据题意，得AE=t，OE=8－t.
∴点Q的纵坐标为
(8－t)，点P的纵坐标为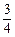
t，
∴PQ= (8－t)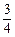－t=10－2t.
当MN在AD上时，10－2t=t，
∴t=
. 6分
当0<t≤时，S=t(10－2t)，即S=－2t2+10t. 7分
当≤t<5时，S=(10－2t)2，即S=4t2－40t+100. 8分
⑶当0<t≤时，S=－2(t－
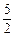)2+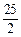
，
∴t=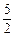时，S最大值=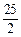. 9分
当≤t<5时，S=4(t－5)2，
∵t<5时，S随t的增大而减小，
∴t=时，S最大值=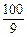
. 11分
∵>，
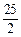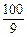解析:
略
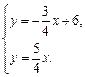
解得
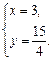
∴C（3,
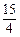）. 3分⑵根据题意，得AE=t，OE=8－t.
∴点Q的纵坐标为
(8－t)，点P的纵坐标为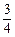t，∴PQ=
(8－t)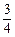－t=10－2t.当MN在AD上时，10－2t=t，
∴t=
. 6分 当0<t≤
时，S=t(10－2t)，即S=－2t2+10t. 7分当
≤t<5时，S=(10－2t)2，即S=4t2－40t+100. 8分 ⑶当0<t≤
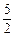时，S=－2(t－)2+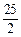，∴t=
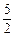时，S最大值=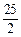. 9分当
≤t<5时，S=4(t－5)2，∵t<5时，S随t的增大而减小，
∴t=
时，S最大值=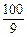. 11分∵
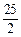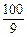>，解析:略
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知：如图，直线y=-x+4分别与x轴，y轴交于A、B两点，从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（ ）
（2012•青浦区二模）如图，直线y=x+1分别与 x轴、y轴分别相交于点A、B．抛物线y=ax2+bx+c（a≠0）与 y轴的正半轴相交于点C，与这个一次函数的图象相交于A、D，且sin∠ACB=
x-3分别与y轴、x轴交于点A，B，抛物线y=-
x2+2x+2与y轴交于点C，此抛物线的对称轴分别与BC，x轴交于点P，Q．
分别与y轴、x轴相交于点A，点B，且AB=5，一个圆心在坐标原点，半径为1的圆，以0.8个单位/秒的速度向y轴正方向运动，设此动圆圆心离开坐标原点的时间为t（t≥0）（秒）．
分别与x轴、y轴交于A、B两点；直线
与AB交于点C，与过点A且平行于y轴的直线交于点D.点E从点A出发，以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）.
）在正方形PQMN内部时t的取值范围.