Question

【题目】如图，以直线AB上一点O为端点作射线OC，使∠BOC=70°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE=90°）

（1）如图①，若直角三角板DOE的一边OD放在射线OB上，则∠COE=　 　°；

（2）如图②，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OC恰好平分∠BOE，求∠COD的度数；

（3）如图③，将直角三角板DOE绕点O转动，如果OD始终在∠BOC的内部，试猜想∠BOD和∠COE有怎样的数量关系？并说明理由．

Answer 1

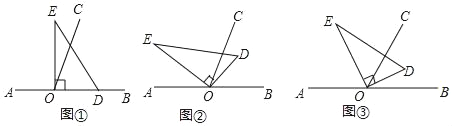
【答案】（1）20；（2）20 ；（3）∠COE﹣∠BOD=20°．

【解析】试题分析：（1）根据图形得出∠COE=∠DOE-∠BOC，代入求出即可；（2）根据角平分线定义求出∠EOB=2∠BOC=140°，代入∠BOD=∠BOE-∠DOE，求出∠BOD，代入∠COD=∠BOC-∠BOD求出即可；（3）根据图形得出∠BOD+∠COD=∠BOC=70°，∠COE+∠COD=∠DOE=90°，相减即可求出答案．

试题解析：

（1）如图①，∠COE=∠DOE﹣∠BOC=90°﹣70°=20°；

（2）如图②，∵OC平分∠EOB，∠BOC=70°，

∴∠EOB=2∠BOC=140°，

∵∠DOE=90°，

∴∠BOD=∠BOE﹣∠DOE=50°，

∵∠BOC=70°，

∴∠COD=∠BOC﹣∠BOD=20°；

（3）∠COE﹣∠BOD=20°，

理由是：如图③，∵∠BOD+∠COD=∠BOC=70°，∠COE+∠COD=∠DOE=90°，

∴（∠COE+∠COD）﹣（∠BOD+∠COD）

=∠COE+∠COD﹣∠BOD﹣∠COD

=∠COE﹣∠BOD

=90°﹣70°

=20°，

即∠COE﹣∠BOD=20°．