题目内容
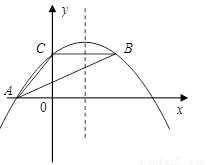
(11分)如图,抛物线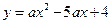 经过
经过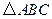 的三个点,已知
的三个点,已知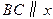 轴,点
轴,点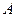 在
在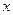 轴上,点
轴上,点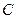 在
在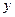 轴上,且
轴上,且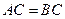 .
.(1)求抛物线的对称轴;
(2)写出
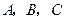 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式;(3)探究:若点
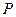 是抛物线对称轴上且在
是抛物线对称轴上且在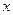 轴下方的动点,是否存在
轴下方的动点,是否存在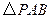 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点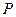 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

解:(1)抛物线的对称轴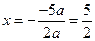 ………2分
………2分
(2)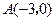
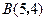
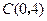 …………5分
…………5分
把点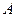 坐标代入
坐标代入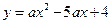 中,解得
中,解得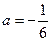 …6分
…6分
 ……………………………7分
……………………………7分
(3)如图所示,存在符合条件的点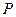 共有3个.……8分
共有3个.……8分
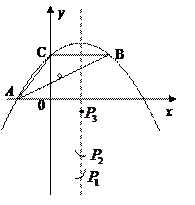

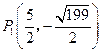 ………………9分
………………9分
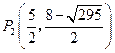 ………………10分
………………10分
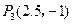 …………11分
…………11分
求P点的详细过程:
以下分三类情形探索.
设抛物线对称轴与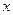 轴交于
轴交于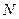 ,与
,与 交于
交于 .
.
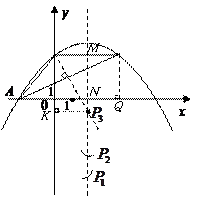

过点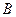 作
作 轴于
轴于 ,易得
,易得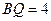 ,
,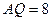 ,
,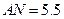 ,
,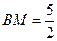
以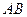 为腰且顶角为角
为腰且顶角为角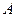 的
的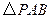 有1个:
有1个: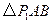 .
.
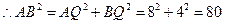 8分
8分
在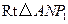 中,
中,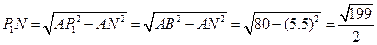
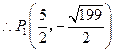 9分
9分
②以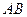 为腰且顶角为角
为腰且顶角为角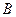 的
的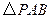 有1个:
有1个: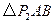 .
.
在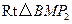 中,
中,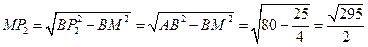 10分
10分
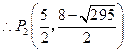 11分
11分
③以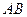 为底,顶角为角
为底,顶角为角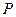 的
的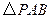 有1个,即
有1个,即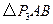 .
.
画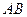 的垂直平分线交抛物线对称轴于
的垂直平分线交抛物线对称轴于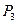 ,此时平分线必过等腰
,此时平分线必过等腰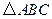 的顶点
的顶点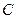 .
.
过点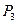 作
作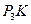 垂直
垂直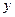 轴,垂足为
轴,垂足为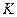 ,显然
,显然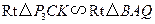 .
.
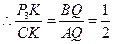 .P3K=2.5,
.P3K=2.5, 于是
于是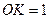 ………………13分
………………13分
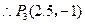 …………14分注:第(3)小题中,只写出点
…………14分注:第(3)小题中,只写出点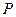 的坐标,无任何说明者不得分.解析:
的坐标,无任何说明者不得分.解析:
略
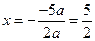 ………2分
………2分(2)
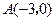
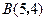
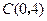 …………5分
…………5分把点
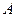 坐标代入
坐标代入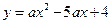 中,解得
中,解得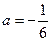 …6分
…6分 ……………………………7分
……………………………7分(3)如图所示,存在符合条件的点
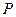 共有3个.……8分
共有3个.……8分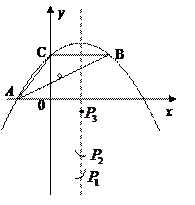

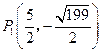 ………………9分
………………9分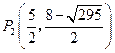 ………………10分
………………10分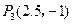 …………11分
…………11分求P点的详细过程:
以下分三类情形探索.
设抛物线对称轴与
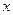 轴交于
轴交于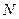 ,与
,与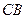 交于
交于 .
.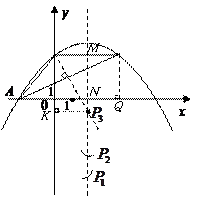

过点
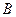 作
作 轴于
轴于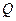 ,易得
,易得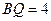 ,
,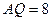 ,
,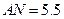 ,
,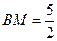
以
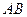 为腰且顶角为角
为腰且顶角为角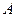 的
的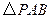 有1个:
有1个: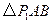 .
.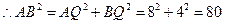 8分
8分在
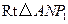 中,
中,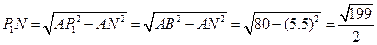
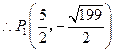 9分
9分②以
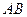 为腰且顶角为角
为腰且顶角为角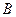 的
的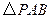 有1个:
有1个: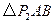 .
.在
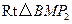 中,
中,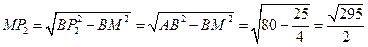 10分
10分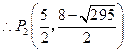 11分
11分③以
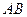 为底,顶角为角
为底,顶角为角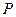 的
的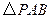 有1个,即
有1个,即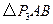 .
.画
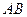 的垂直平分线交抛物线对称轴于
的垂直平分线交抛物线对称轴于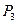 ,此时平分线必过等腰
,此时平分线必过等腰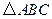 的顶点
的顶点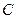 .
.过点
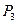 作
作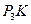 垂直
垂直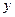 轴,垂足为
轴,垂足为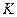 ,显然
,显然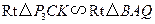 .
.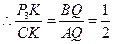 .P3K=2.5,
.P3K=2.5, 于是
于是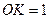 ………………13分
………………13分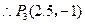 …………14分注:第(3)小题中,只写出点
…………14分注:第(3)小题中,只写出点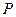 的坐标,无任何说明者不得分.解析:
的坐标,无任何说明者不得分.解析:略

练习册系列答案
相关题目
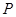 是抛物线对称轴上且在
是抛物线对称轴上且在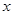 轴下方的动点,是否存在
轴下方的动点,是否存在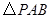 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点

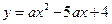 经过
经过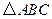 的三个点,已知
的三个点,已知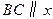 轴,点
轴,点 在
在 轴上,点
轴上,点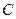 在
在 轴上,且
轴上,且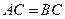 .
.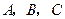 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式; 是抛物线对称轴上且在
是抛物线对称轴上且在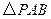 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点

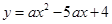 经过
经过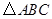 的三个点,已知
的三个点,已知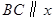 轴,点
轴,点 在
在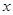 轴上,点
轴上,点 在
在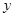 轴上,且
轴上,且 .
.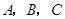 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式; 是抛物线对称轴上且在
是抛物线对称轴上且在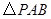 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点