题目内容
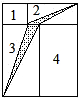 用面积为1,2,3,4的4张长方形纸片拼成如下图所示的一个大长方形.问:图中阴影部分面积是多少?
用面积为1,2,3,4的4张长方形纸片拼成如下图所示的一个大长方形.问:图中阴影部分面积是多少?
分析:设面积为1的长方形长、宽分别为a、b,则ab=1,根据面积发分别计算面积为2、3、4的长、宽,用a、b表示阴影部分的面积,即可解题.
解答: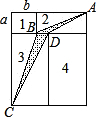 解:设面积为1的长方形长、宽分别为a、b,则ab=1
解:设面积为1的长方形长、宽分别为a、b,则ab=1
面积为2的长方形宽为a,长为
,
面积为3的长方形和面积为4的长方形的长相等,则宽的比例为3:4,
故面积为3的长方形的宽为
(b+
)=
×
=
,长为
=
,
BD=
-b.
阴影部分的面积为△ABD和△BCD面积之和,
∴阴影部分的面积为
×(
-b)×(
+a)=
,
答:图中阴影部分面积是
.
 解:设面积为1的长方形长、宽分别为a、b,则ab=1
解:设面积为1的长方形长、宽分别为a、b,则ab=1面积为2的长方形宽为a,长为
| 2 |
| a |
面积为3的长方形和面积为4的长方形的长相等,则宽的比例为3:4,
故面积为3的长方形的宽为
| 3 |
| 3+4 |
| 2 |
| a |
| 3 |
| 7 |
| ab+2 |
| a |
| 9 |
| 7a |
| 3 | ||
|
| 7a |
| 3 |
BD=
| 9 |
| 7a |
阴影部分的面积为△ABD和△BCD面积之和,
∴阴影部分的面积为
| 1 |
| 2 |
| 9 |
| 7a |
| 7a |
| 3 |
| 10 |
| 21 |
答:图中阴影部分面积是
| 10 |
| 21 |
点评:本题考查了长方形面积的计算,考查了三角形面积的计算,本题中求BD的长是解题的关键.

练习册系列答案
相关题目
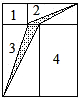 用面积为1,2,3,4的4张长方形纸片拼成如下图所示的一个大长方形.问:图中阴影部分面积是多少?
用面积为1,2,3,4的4张长方形纸片拼成如下图所示的一个大长方形.问:图中阴影部分面积是多少?