题目内容
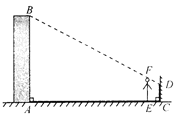
【题目】如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37° ≈ 0.6,cos37°≈ 0.8,tan37° ≈ 0.75)


【答案】小桌板桌面的宽度BC约为37.5cm.
【解析】试题分析:延长CB交AO于点D.则CD⊥OA,在Rt△OBD中根据正弦函数求得BD,根据余弦函数求得OD,在Rt△ACD中,根据正切函数求得AD,然后根据AD+OD=OA=75,列出关于x的方程,解方程即可求得.
试题解析:延长CB交AO于点D.

∴CD⊥OA,
设BC=x,则OB=75-x,
在Rt△OBD中,OD=OBcos∠AOB,BD=OBsin∠AOB,
∴OD=(75-x)cos37°=0.8(75-x)=60-0.8x,
BD=(75-x)sin37°=0.6(75-x)=45-0.6x,
在Rt△ACD中,AD=DCtan∠ACB,
∴AD=(x+45-0.6x)tan37°=0.75(0.4x+45)=0.3x+33.75,
∵AD+OD=OA=75,
∴0.3x+33.75+60-0.8x=75,
解得x=37.5.
∴BC=37.5;
故小桌板桌面的宽度BC约为37.5cm.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目