题目内容
(本题12分)从A、B两水库向甲乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14吨,从A地到甲地50千米,到乙地30千米,从B地到甲地60千米,到乙地45千米,设计一个调运方案使水的调运量(单位:万吨.千米)尽可能小。
从A调往甲1万吨水,调往乙13万吨水;从B调往甲14万吨水。
分析:本题用到的关系是:调运量=调运吨数×调运的路程.本题可根据该关系求出总共的调运量。
解答:
设A水库向甲地调水为x万吨,则A水库向乙地调水为(14-x)万吨;
则B水库向甲地调水为15-x万吨,则B水库向乙地调水为(14-(15-x)=x-1)万吨。
要保证都有意义,则1≤x≤14;
所以总共的调运量为y=50x+30(14-x)+60(15-x)+45(x-1)=5x+1275(其中1≤x≤14)
要得到最小值应该取x=1。
所以设计的调水方案为A水库向甲地调水1万吨,向乙地调水13万吨;B水库向甲地调水14万吨,向乙地调水0万吨。
点评:此题主要考查利用一次函数的模型解决实际问题的能力。要先根据题意列出函数关系式,再代数求值。解题的关键是要分析题意根据实际意义求解,注意要根据自变量的实际范围确定函数的最值。

练习册系列答案
相关题目
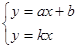 的解是
的解是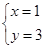 ,则一次函数y=ax+b与y=kx的交点P的坐标是 ____ ______
,则一次函数y=ax+b与y=kx的交点P的坐标是 ____ ______



 的解也是二元一次方程
的解也是二元一次方程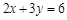 的解,则k 的值为_______。
的解,则k 的值为_______。 的解是 .
的解是 .  满足
满足 ,求
,求 的平方根.
的平方根. 可得出
可得出 与
与 的关系是( )
的关系是( )


