题目内容
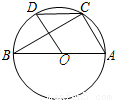
（2008•广东）如图，已知AB是⊙O的直径，BC为弦，∠ABC=30度．过圆心O作OD⊥BC交BC于点D，连接DC，则∠DCB= 度．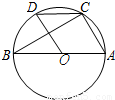
【答案】分析：先根据直角三角形两锐角互余求出∠BOD，再根据圆周角定理∠DCB=
∠BOD．
解答：解：∵OD⊥BC交BC于点D，∠ABC=30°，
∴∠BOD=90°-∠ABC=90°-30°=60°，
∴∠DCB=
∠BOD=30°．
点评：本题的关键是利用直角三角形两锐角互余和圆周角定理．
∠BOD．解答：解：∵OD⊥BC交BC于点D，∠ABC=30°，
∴∠BOD=90°-∠ABC=90°-30°=60°，
∴∠DCB=
∠BOD=30°．点评：本题的关键是利用直角三角形两锐角互余和圆周角定理．
练习册系列答案
名校课堂系列答案
相关题目
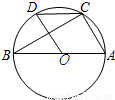
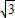是指坡面的铅直高度DE与水平宽度CE的比），∠B=60°，AB=6，AD=4，求拦水坝的横断面ABCD的面积．（结果保留三位有效数字．参考数据：
≈1．732，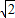
≈1.414）
