题目内容
 (2008•宝山区二模)已知∠AOB=45°,P是边OA上一点,OP=4
(2008•宝山区二模)已知∠AOB=45°,P是边OA上一点,OP=4| 2 |
| PD |
| DQ |
| 2 |
| 3 |
(1)求圆P半径长;
(2)当点Q在射线OB上运动时,以点Q为圆心,OQ为半径作圆Q,若圆Q与圆P相切,试求OQ的长度;
(3)连CD并延长交直线OB于点E,是否存在这样的点Q,使得以O、C、E为顶点的三角形与△OPQ相似?若存在,试确定Q点的位置;若不存在,试说明理由.
分析:(1)首先过点P作PG⊥OB,垂足为G,由∠AOB=45°,OP=4
,根据勾股定理,即求得PG与OG的值,又由OQ=7,
=
,即可求得PD的长;
(2)首先设OQ=x,根据勾股定理可得PQ=
,然后分别从⊙P与⊙Q外切或外切去分析求解即可求得答案;
(3)首先易得∠POQ=∠COE,∠OPQ=2∠OCE≠∠OCE,可得要使△OPQ与△OCE相似,只可能∠OQP=∠OCE,然后分别从当点Q在射线OB上时与当点Q在射线OB的反向延长线上时去分析求解即可求得答案.
| 2 |
| PD |
| DQ |
| 2 |
| 3 |
(2)首先设OQ=x,根据勾股定理可得PQ=
| x2-8x+32 |
(3)首先易得∠POQ=∠COE,∠OPQ=2∠OCE≠∠OCE,可得要使△OPQ与△OCE相似,只可能∠OQP=∠OCE,然后分别从当点Q在射线OB上时与当点Q在射线OB的反向延长线上时去分析求解即可求得答案.
解答: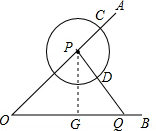 解:(1)过点P作PG⊥OB,垂足为G,
解:(1)过点P作PG⊥OB,垂足为G,
∵∠AOB=45°,OP=4
,
∴PG=OG=4. …(1分)
又∵OQ=7,
∴GQ=3.
从而PQ=5,…(1分)
∵
=
,
∴PD=2,
即⊙的半径长为2.…(1分)
(2)设OQ=x,则PQ=
=
. (1分)
当⊙P与⊙Q外切时,
PQ=OQ+2,即
=x+2,…(1分)
解得:x=
.经检验是方程的根,且符合题意,…(1分)
当⊙P与⊙Q 内切时,
PQ=OQ-2,即
=x-2,…(1分)
解得:x=7.经检验是方程的根,且符合题意,…(1分)
所以,当OQ的长度为
或7时,⊙P与⊙Q相切.
(3)∵∠POQ=∠COE,
∵PC=PD,
∴∠PDC=∠PCD,从而∠OPQ=2∠OCE≠∠OCE,
∴要使△OPQ与△OCE相似,只可能∠OQP=∠OCE,…(1分)
当点Q在射线OB上时,
∠OQP=45°,∠OPQ=90°.
∴OQ=8.…(2分)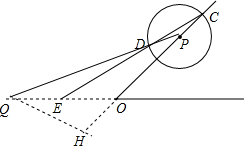
当点Q在射线OB的反向延长线上时,
∠OQP=15°,∠OPQ=30°.
过点Q作QH⊥OP,垂足为H,
则 PH=
QH,
设 QH=t,则t+4
=
t,
解得:t=2
+2
,
∴OQ=
t=4
+4.…(2分)
综上,点Q在射线OB上,且OQ=8时,以O、C、E为顶点的三角形与△OPQ相似;或者点Q在射线OB的反向延长线上,且OQ=4
+4时,以O、C、E为顶点的三角形与△OPQ相似.
 解:(1)过点P作PG⊥OB,垂足为G,
解:(1)过点P作PG⊥OB,垂足为G,∵∠AOB=45°,OP=4
| 2 |
∴PG=OG=4. …(1分)
又∵OQ=7,
∴GQ=3.
从而PQ=5,…(1分)
∵
| PD |
| DQ |
| 2 |
| 3 |
∴PD=2,
即⊙的半径长为2.…(1分)
(2)设OQ=x,则PQ=
| (x-4)2+42 |
| x2-8x+32 |
当⊙P与⊙Q外切时,
PQ=OQ+2,即
| x2-8x+32 |
解得:x=
| 7 |
| 3 |
当⊙P与⊙Q 内切时,
PQ=OQ-2,即
| x2-8x+32 |
解得:x=7.经检验是方程的根,且符合题意,…(1分)
所以,当OQ的长度为
| 7 |
| 3 |
(3)∵∠POQ=∠COE,
∵PC=PD,
∴∠PDC=∠PCD,从而∠OPQ=2∠OCE≠∠OCE,
∴要使△OPQ与△OCE相似,只可能∠OQP=∠OCE,…(1分)
当点Q在射线OB上时,
∠OQP=45°,∠OPQ=90°.
∴OQ=8.…(2分)

当点Q在射线OB的反向延长线上时,
∠OQP=15°,∠OPQ=30°.
过点Q作QH⊥OP,垂足为H,
则 PH=
| 3 |
设 QH=t,则t+4
| 2 |
| 3 |
解得:t=2
| 6 |
| 2 |
∴OQ=
| 2 |
| 3 |
综上,点Q在射线OB上,且OQ=8时,以O、C、E为顶点的三角形与△OPQ相似;或者点Q在射线OB的反向延长线上,且OQ=4
| 3 |
点评:此题考查了相似三角形的判定与性质、勾股定理、圆与圆的位置关系等知识.此题综合性很强,难度较大,解题的关键注意方程思想与数形结合思想的应用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (2008•宝山区二模)甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图中信息,下列说法中,不正确的是( )
(2008•宝山区二模)甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图中信息,下列说法中,不正确的是( )