题目内容
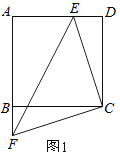
【题目】如图1，正方形ABCD的边长为6cm，点F从点B出发，沿射线AB方向以1cm/秒的速度移动，点E从点D出发，向点A以1cm/秒的速度移动（不到点A）．设点E，F同时出发移动t秒．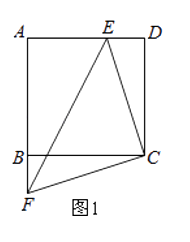
（1）在点E，F移动过程中，连接CE，CF，EF，则△CEF的形状是 ， 始终保持不变；
（2）如图2，连接EF，设EF交BD移动M，当t=2时，求AM的长；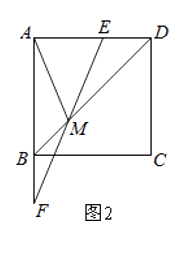
（3）如图3，点G，H分别在边AB，CD上，且GH=3 
cm，连接EF，当EF与GH的夹角为45°，求t的值．
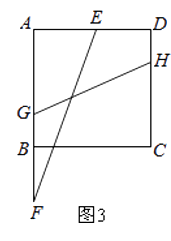
【答案】
（1）等腰直角三角形
（2）解：如图2，过点E作EN∥AB，交BD于点N，则∠NEM=∠BFM．
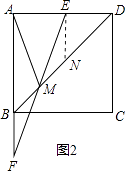
∴∠END=∠ABD=∠EDN=45°，
∴EN=ED=BF．
在△EMN与△FMB中，
，
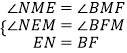∴△EMN≌△FMB（AAS），
∴EM=FM．
∵Rt△AEF中，AE=4，AF=8，
∴ 
=EF= 
=4 
，
∴AM= 
EF=2
（3）解：如图3，连接CE，CF，设EF与GH交于P．
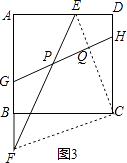
由（1）得∠CFE=45°，又∠EPQ=45°，
∴GH∥CF，
又∵AF∥DC，
∴四边形GFCH是平行四边形，
∴CF=GH=3 ，
在Rt△CBF中，得BF= 
= 
=3，
∴t=3．
【解析】解：（1）等腰直角三角形．理由如下：
如图1，在正方形ABCD中，DC=BC，∠D=∠ABC=90°．
依题意得：DE=BF=t．
在△CDE与△CBF中，
，
∴△CDE≌△CBF（SAS），
∴CF=CE，∠DCE=∠BCF，
∴∠ECF=∠BCF+∠BCE=∠DCE+∠BCE=∠BCD=90°，
∴△CEF是等腰直角三角形．
故答案是：等腰直角三角形．
【考点精析】本题主要考查了等腰直角三角形的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°才能正确解答此题．
