题目内容
一个人由山底爬到山顶，需先爬30°的山坡80m，再爬40°的山坡300m，则山高为 m．
考点：解直角三角形的应用-坡度坡角问题
专题：计算题
分析：作出图形，根据行走的距离和山坡与水平地面的夹角即可求得AB、DE，再计算AB+DE即得到山的高度．
解答：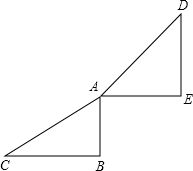
解：如图，
∠ACB=30°，∠DAE=40°，
∴AB=AC•sinC=80×
=40m，
DE=AD•sin40°=300sin40°m，
∴山的高度为（300sin40°+40）m．
故答案为（300sin40°+40）m．
解：如图，∠ACB=30°，∠DAE=40°，
∴AB=AC•sinC=80×
| 1 |
| 2 |
DE=AD•sin40°=300sin40°m，
∴山的高度为（300sin40°+40）m．
故答案为（300sin40°+40）m．
点评：本题考查了解直角三角形--坡度和坡角问题，熟悉坡度的定义三角函数的定义并能灵活运用是解题的关键．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
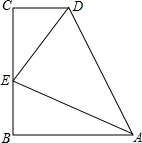如图，在梯形ABCD中，AB∥CD，E是BC的中点，AB+CD=AD，求证：
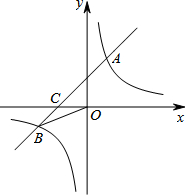已知：如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数
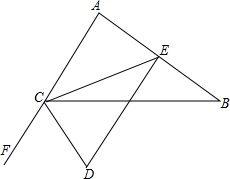如图，已知CE是△ABC的中线，DE⊥AB交外角∠BCF的平分线于D，∠ACB=60°，证明：BC=AC+CD．
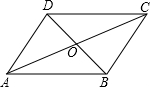如图，在?ABCD中，对角线AC、BD相交于点O．如果AB=8，AC=14，BD=x，那么x的取值范围是
如图，△ABC中，∠A=60°，则∠1+∠2的度数为（ ）| A、120° | B、180° |
| C、240° | D、300° |