题目内容
已知mn＜0，点P（m，n）在反比例函数y=
的图象上，则直线y=mx+n不经过（ ）
| m |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
分析：将P（m，n）代入y=
得，n=
=1；则直线方程变为y=mx+1；又因为mn＜0，所以m＜0；根据m、n的值确定一次函数y=mx+n的图象经过的象限．
| m |
| x |
| m |
| m |
解答：解：将P（m，n）代入y=
得，n=
=1，
则直线方程变为y=mx+1，
又因为mn＜0，所以m＜0，
根据一次函数的性质，y=mx+1（m＜0）过一二四象限．
故选C．
| m |
| x |
| m |
| m |
则直线方程变为y=mx+1，
又因为mn＜0，所以m＜0，
根据一次函数的性质，y=mx+1（m＜0）过一二四象限．
故选C．
点评：本题综合考查了反比例函数和一次函数的性质，先求出m、n的值或取值范围，再进行判断．
练习册系列答案
相关题目
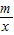的图象上，则直线y=mx+n不经过（ ）