��Ŀ����
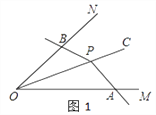
����Ŀ����ͼ1��PΪ��MONƽ����OC��һ�㣬��PΪ�������APB���߷ֱ�������OM��ON����A��B���㣬�����APB���Ƶ�P��תʱʼ������OAOB=OP2 �� ���ǾͰ���APB������MON�Ĺ����ǣ�
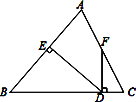
��1����ͼ2��PΪ��MONƽ����OC��һ�㣬��P��PB��ON��B��AP��OC��P����ô��APB________��MON�Ĺ����ǣ�����������������������
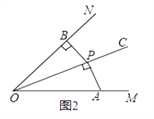
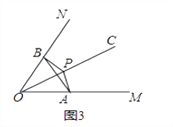
��2������ͼ3�������MON=60�㣬OP=2����APB����MON�Ĺ����ǣ�����AB������AOB���������APB�Ķ�����
�������MON=���㣨0�㣼���㣼90�㣩��OP=m����APB����MON�Ĺ����ǣ�ֱ���ú�������m�Ĵ���ʽ��ʾ��AOB�������
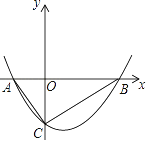
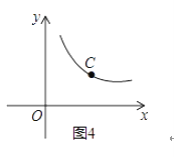
��3����ͼ4����C�Ǻ���y=![]() ��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ�������APB�Ķ���P�����꣮
��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ�������APB�Ķ���P�����꣮
���𰸡���
�������������������1�����жϳ���OBP�ס�OPA�����ɣ�
��2���ȸ��ݹ��������OA��OB=4�������������ε������ʽ���Լ����ƣ��õ���OAP=��OPB�����ɣ�
��3������������������ۣ���B��y������������ᣬ�ڸ�����ʱ���������㣬�����ڣ�����������ʱ����BC=2AC�жϳ���C���߶�AB��һ�����ȷֵ㣬���ɣ�
�����������1����PΪ��MONƽ����OC��һ�㣬
���BOP=��AOP��
��PB��ON��B��AP��OC��P��
���OBP=��OPA��
���OBP�ס�OPA��
��![]() ��
��
��OP2=OA��OB��
���APB�ǡ�MON�Ĺ����ǣ�
�ʴ�Ϊ�ǣ�
��2������ͼ������A��AH��OB��
�ߡ�APB�ǡ�MON�Ĺ����ǣ�OP=2��
��OA��OB=OP2=4��
��Rt��AOH����AOH=90����
��sin��AOH=![]() ��
��
��AH=OAsin��AOH��
��S��AOB=![]() OB��AH=
OB��AH=![]() OB��OA��sin60��=
OB��OA��sin60��=![]() ��OP2��
��OP2��![]() =
=![]() ��
��
��OP2=OA��OB��
��![]() ��
��
�ߵ�PΪ��MON��ƽ������һ�㣬
���AOP=��BOP=![]() ��MON=30����
��MON=30����
���AOP�ס�POB��
���OAP=��OPB��
���APB=��OPB+��OPA=��OAP+��OPA=180��-30��=150����
���ɢ��У�S��AOB=![]() OB��OA����MON=
OB��OA����MON=![]() m2��sin����
m2��sin����
��3���߹���C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��
��ֻ�е�A��x�������ᣬ
�ٵ���B��y�Ḻ����ʱ����Aֻ����x�������ᣮ������Pֻ���ڵ������ޣ�
��A��m��0����B��0��n����m��0��n��0��
��OA=m��OB=-n��
��BC=2CA��
���A��BC�е㣬
���C��2m��-n����
�ߵ�C��˫����y=![]() �ϣ�
�ϣ�
��2m����-n��=2��
��mn=-1��
�ߡ�AOB�Ĺ����ǡ�APB
��OP2=OA��OB=|m||n|=1span>��
��OP=1��
�ߵ�P�ڡ�AOB��ƽ�����ϣ���P��a��-a����a��0����
��OP2=2a2��
��2a2=1��
��a=![]() ��a=-
��a=-![]() ���ᣩ��
���ᣩ��
���P��![]() ��-
��-![]() ��
��
�ڵ���B��y�������ᣬ����BC=2CA�����ԣ���Aֻ����x���������ϣ�
��A��m��0����B��0��n����m��0��n��0��
���C��![]() ��
�� ![]() ����
����
��![]() ��
��![]() =2��
=2��
��mn=9��
�ߡ�AOB�Ĺ����ǡ�APB
��OP2=OA��0B=mn=9��
��OP=3��
�ߵ�P�ڡ�AOB��ƽ�����ϣ�������P�ڵ�һ���ޣ���P��a��a������a��0��
��OP2=2a2��
��2a2=9��
��a=![]() ��a=-
��a=-![]() ���ᣩ
���ᣩ
������P��![]() ��
�� ![]() ����
����
������������P����������![]() ��-
��-![]() ������
������![]() ��
�� ![]() ����
����

����Ŀ���ӹ������������������ȹ������е�������ɡ�ȹ�����Ʒ����ʽ�����Ĺ�������ģʽ�ڸ�������Ѹ�ٵ��ռ���
(1) Ϊ��ö�̨��������빲�����õĻ��Ϣ�����е��鷽ʽ�бȽϺ��������� ����
A����ijѧУ��ȫ��ͬѧ�����ʾ�����
B����ijС����ס�������ʾ�����
C����ȫ����IJ�ͬ������ѡȡ������������ʾ�����
(2) ����С����������˶�̨�����ﹲ�����������ij����������12��36�������1000�ˣ����������ȡ��100�ˣ�ͳ���������ﹲ�������������������������²�������ͳ��ͼ����
�ﹲ������������ͳ�Ʊ�
�����(��) | Ƶ�� | Ƶ�� |
12��x��16 | 2 | 0.02 |
16��x��20 | 3 | 0.03 |
20��x��24 | 15 | a |
24��x��28 | 25 | 0.25 |
28��x��32 | b | 0.30 |
32��x��36 | 25 | 0.25 |
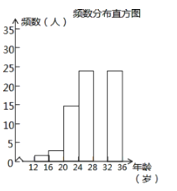
����������Ϣ����������⣺
�� ���ͳ�Ʊ��е�a��b������ȫƵ���ֲ�ֱ��ͼ��
�� �Թ����������������20�굽32��(��20�꣬����32��)�ﹲ�����������ж����ˣ�