题目内容
【题目】已知A、B、C不在同一直线上,顺次连接AB、BC、CA.
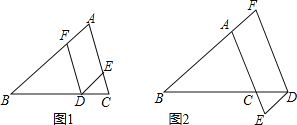
(Ⅰ)如图①,点D在线段BC上,DE∥AB交AC于点E,∠EDF=∠A.求证:DF∥AC.
(Ⅱ)如图②,若点D在BC的延长线上,DE∥AB交AC的延长线于点E,DF∥AC交BA的延长线于点F.问∠EDF与∠BAC有怎样的关系,说明理由.
【答案】(Ⅰ)见解析(Ⅱ)∠EDF与∠BAC互补
【解析】
试题分析:(1)先根据平行线的性质,得出∠EDF=∠BFD,再根据∠EDF=∠A,得出∠A=∠BFD即可得出结论;
(2)先根据DE∥AB得出∠EDF与∠F互补,再根据DF∥AC得出∠F=∠BAC,即可得出结论.
解:(1)∵DE∥AB
∴∠EDF=∠BFD
又∵∠EDF=∠A
∴∠A=∠BFD
∴DF∥AC
(2)∠EDF与∠BAC互补
∵DE∥AB
∴∠EDF与∠F互补
∵DF∥AC
∴∠F=∠BAC
∴∠EDF与∠BAC互补

练习册系列答案
相关题目
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率;
(2)小颖说:“根据上述实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”,小颖和小红的说法正确吗?为什么?