Question

【题目】已知等腰三角形一腰上的中线将它的周长分成9cm和12cm两部分，则等腰三角形的底边长为（ ）
A.9cm
B.5cm
C.6cm或5cm
D.5cm或9cm

Answer 1

【答案】D
【解析】根据题意画出图形，如图所示，

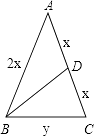
设等腰三角形的腰长AB=AC=2x，BC=y，

∵BD是腰上的中线，∴AD=DC=x,①若AB+AD的长为12，则2x+x=12，解得x=4，则x+y=9，即4+y=9，解得y=5，所以等腰三角形的底边为5；②若AB+AD的长为9，则2x+x=9，解得x=3，则x+y=12，即3+y=12，解得y=9，所以等腰三角形的底边为9；

所以答案是：D.

【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识，掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．