题目内容
如图,已知椭圆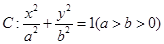 的焦点和上顶点分别为
的焦点和上顶点分别为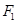 、
、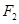 、
、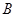 ,我们称
,我们称 为椭圆
为椭圆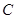 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.(1)已知椭圆
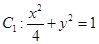 和
和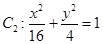 ,判断
,判断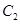 与
与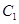 是否相似,如果相似则求出
是否相似,如果相似则求出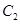 与
与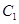 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;(2)若与椭圆
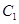 相似且半短轴长为
相似且半短轴长为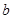 的椭圆为
的椭圆为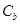 ,且直线
,且直线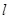 与椭圆为
与椭圆为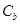 相交于两点
相交于两点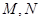 (异于端点),试问:当
(异于端点),试问:当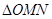 面积最大时,
面积最大时,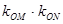 是否与
是否与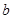 有关?并证明你的结论.
有关?并证明你的结论.(3)根据与椭圆
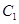 相似且半短轴长为
相似且半短轴长为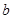 的椭圆
的椭圆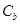 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);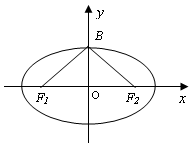
见解析.解析:
第一问中利用根据已知的的定义进行判定特征三角形是否相似即可
第二问中,设直线方程,借助于联立方程组,和韦达定理可以表示斜率之积,然后可知为定植
第三问中,利用类比推理的思想可知两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比
解:(1)由题意可知,椭圆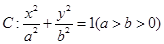 的焦点和上顶点分别为
的焦点和上顶点分别为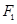 、
、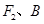 ,我们称
,我们称 为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆
为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆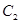 与
与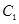 相似. ………2分
相似. ………2分
因为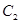 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为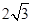 的等腰三角形,
的等腰三角形,
而椭圆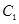 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为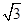 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为2:1 ……… 4分
(2)椭圆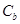 的方程为:
的方程为: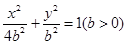 .
.
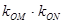 =
=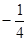 与b无关 -----------6分
与b无关 -----------6分
(3)椭圆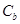 的方程为:
的方程为: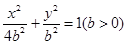 .
.
两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ---------------6分
第一问中利用根据已知的的定义进行判定特征三角形是否相似即可
第二问中,设直线方程,借助于联立方程组,和韦达定理可以表示斜率之积,然后可知为定植
第三问中,利用类比推理的思想可知两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比
解:(1)由题意可知,椭圆
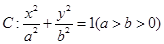 的焦点和上顶点分别为
的焦点和上顶点分别为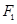 、
、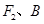 ,我们称
,我们称 为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆
为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆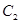 与
与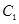 相似. ………2分
相似. ………2分因为
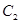 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为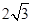 的等腰三角形,
的等腰三角形,而椭圆
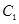 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为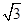 的等腰三角形,
的等腰三角形,因此两个等腰三角形相似,且相似比为2:1 ……… 4分
(2)椭圆
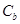 的方程为:
的方程为: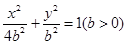 .
. 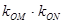 =
=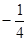 与b无关 -----------6分
与b无关 -----------6分(3)椭圆
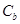 的方程为:
的方程为: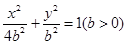 .
. 两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ---------------6分

练习册系列答案
相关题目